Az RDF Szemantikája
(Ez a fordítás a W3C Magyar Irodájának megbízásából,
az
Informatikai és Hírközlési Minisztérium
támogatásával készült)
- Az eredeti dokumentum:
- RDF
Semantics
- http://www.w3.org/TR/2004/REC-rdf-mt-20040210/
- A lefordított dokumentum:
- http://www.w3c.hu/forditasok/RDF/REC-rdf-mt-20040210.html
- Magyar fordítás (Hungarian translation):
- Pataki, Ernő 2005 (pataki.erno@w3c.hu)
- A fordítás státusa:
- Kézirat. Lezárva: 2005.04.13.
Utoljára módosítva: 2005.04.25.
- Ez a fordítás a W3C engedélyével, a
fordításokra előírt formai szabályok szerint, lelkiismeretes
szakfordítói munkával készült. Ennek ellenére nem lehet kizárni, hogy
hibák maradtak a fordításban. Emellett a magyar fordítás nem is követi
feltétlenül az eredeti angol nyelvű dokumentumon végrehajtott jövőbeli
változtatásokat. Ezért a fordítás nem tekinthető normatív W3C
dokumentumnak. A dokumentum normatív, mindenkori legújabb,
hivatalos, angol nyelvű változatát lásd a W3C megfelelő weblapján: http://www.w3.org/TR/rdf-mt/
- Megjegyzések a fordításhoz:
- 1.) A fordítással kapcsolatos olvasói észrevételeket a fordító e-mail
címére kérjük.
2.) A fordító a saját megjegyzéseit feltűnően elkülöníti a dokumentum
szövegében.
3.) A fordítással kapcsolatos további információkat, valamint a
terminológiai kérdések diszkusszióját lásd a Köszönetnyilvánítás és
megjegyzések a magyar fordításhoz c. mellékletben.
4.) A W3C Magyar Irodája a lehetőségek szerint lefordíttatja az OWL-ra
és az RDF-re vonatkozó W3C ajánlások legtöbb dokumentumát. Ha tehát egy
lefordított dokumentumból olyan OWL vagy RDF dokumentumra történik
hipertext-hivatkozás, mely magyar változatban is rendelkezésre áll,
akkor a megfelelő link általában a magyar változatra mutat. A kivételt
azok a hivatkozások képezik, amelyeknek a W3C szándékai szerint
mindenképpen az eredeti dokumentumra kell mutatniuk.
Absztrakt
Ez egy pontos szemantikai specifikáció, mely az Erőforrás Leíró
Keretrendszer (RDF), és az RDF Séma (RDFS) következtetési szabályainak
komplett rendszerét definiálja.
Ezt a dokumentumot a W3C tagjai és más érdekelt résztvevők ellenőrizték,
és az Igazgató W3C
Ajánlásként hitelesítette. Az Ajánlás elkészítésével a W3C célja és
szerepe az, hogy ráirányítsa a figyelmet a specifikációra, és elősegítse
annak széles körű alkalmazását. Ez megnöveli a Web használhatóságát, és
javítja a weben történő együttműködést.
Ez a dokumentum egyike annak a hat
dokumentumnak (Bevezetés, Fogalmak, Szintaxis, Szemantika, Szókészlet és Tesztsorozat), amelyek együttesen
felváltják az eredeti Resource Description Framework specifikációkat: az RDF Model and
Syntax (1999 Recommendation) és az RDF Schema (2000
Candidate Recommendation) című dokumentumokat. A jelen dokumentumot az RDF Core Working Group (RDF-mag
Munkacsoport) dolgozta ki a W3C
Szemantikus Web Munkaprogramja keretében, és 2004. február 10. dátummal
publikálta. (Lásd a Munkaprogram-nyilatkozatot és a
Munkacsoport
alapszabályát).
Az Előzetes Ajánlástervezet munkaanyag óta a jelen Ajánlás
megszületéséig a dokumentumon végrehajtott módosításokat a Változtatási napló részletezi.
A Munkacsoport szívesen fogadja az olvasóközönség észrevételeit a www-rdf-comments@w3.org (archive)
címén; az idevágó technológiák általános vitáját pedig a www-rdf-interest@w3.org (archive) címén folytatja.
Rendelkezésre áll egy konszignáció az ismert
alkalmazásokról.
A W3C listát vezet továbbá azokról a felfedett szabadalmi igényekről is, amelyek ehhez a
munkához kapcsolódnak.
Ez a szekció a dokumentumnak a publikáláskor érvényes státusát
rögzíti. Más dokumentumok hatálytalaníthatják ezt a dokumentumot. A legújabb
W3C publikációk listája, valamint e technikai riport utolsó kiadása
megtalálható a W3C technikai riportok
indexében, a http://www.w3.org/TR/ alatt.
Tartalomjegyzék
0. Bevezetés
0.1 Egy formális szemantika
specifikálása – hatókör és korlátok
0.2 A gráfok
szintaxisa
0.3 A gráfokra vonatkozó
definíciók
1. Interpretációk
1.1 Technikai megjegyzések
(Informatív)
1.2 URI hivatkozások,
erőforrások és literálok
1.3 Interpretációk
1.4 Az alapgráfok
jelentése
1.5 Az üres csomópontok mint
egzisztenciális változók
2. Egyszerű következményviszony két RDF gráf között
2.1
Szókészlet-interpretációk és szókészlet-következmények
3. Az RDF szókészlet interpretálása
3.1
RDF-interpretációk
3.2
RDF-következmény
3.3 Tárgyiasítás,
konténerek, kollekciók és az rdf:value
3.3.1
Tárgyiasítás
3.3.2 RDF
konténerek
3.3.3 RDF
kollekciók
3.3.4
rdf:value
4. Az RDFS szókészlet interpretálása
4.1
RDFS-interpretációk
4.2 Extenzionális
szemantikai feltételek (Informatív)
4.3 Egy megjegyzés az
rdfs:Literal-ról
4.4
RDFS-következmény
5. Az adattípusok interpretálása
5.1 A tipizált adatok
értelmezése
5.2 A
D-következmény
6. A szemantikai kiterjesztések monotonitása
7. A következtetés szabályai
(Informatív)
7.1 Az egyszerű következmény
szabályai
7.2 Az RDF-következmény
szabályai
7.3 Az RDFS-következmény
szabályai
7.3.1 Az
extenzionális következmény szabályai
7.4 Az adattípus-következmény
szabályai
A. függelék: A lemmák bizonyítása (Informatív)
B. függelék: A szakkifejezések glosszáriuma
(Informatív)
C. függelék: Köszönetnyilvánítás
A hivatkozások listája
D. függelék: Változtatási napló (Informatív)
Az RDF egy olyan deklaratív nyelv, amelyet állításoknak precíz formális szókészletek
segítségével történő kifejezésére, weben keresztüli elérésére és
alkalmazására fejlesztettek ki. Az ilyen (felhasználói) szókészleteket pedig
egy másik, egy alapvető szókészlet, konkrétan az [RDF-SZÓKÉSZLET] (RDFS) segítségével
lehet specifikálni. Az RDF-et eleve azzal a szándékkal dolgozták ki, hogy
közvetlen alapul szolgáljon más, hasonló célú, de jóval fejlettebb deklaratív
nyelvek ráépítéséhez is. Az átfogó tervezési célok az általánosságra és a
pontosságra teszik a hangsúlyt a bármilyen témakörben tehető állítások
kifejezésében, és nem próbálnak meg alkalmazkodni semmilyen konkrét
feldolgozási modellhez. (Ennek részletesebb diszkusszióját lásd Az RDF alapfogalmai és absztrakt
szintaxisa [RDF-FOGALMAK]
című dokumentumban.)
Az, hogy szélesebb értelemben pontosan mit tekintünk az RDF-ben
vagy RDFS-ben megfogalmazott állítások 'jelentésének', az nagymértékben a
társadalmi konvencióktól, a természetes nyelvű magyarázatoktól, és a más
dokumentumokra való hivatkozásoktól függ. Az ilyen jelentések legtöbbje
hozzáférhetetlen a gépi feldolgozás számára, és csak azért említjük meg itt,
hogy hangsúlyozzuk: az a formális
szemantika, amelyet ebben a
dokumentumban leírunk, nem arra készült, hogy ebben a szélesebb értelemben
adja meg a 'jelentés' komplett elemzését; ez csak egy sokkal nagyobb kutatási
terület témája lehetne. Az itt megadott szemantika a jelentés formális fogalmára korlátozódik, amit
úgy lehetne jellemezni, hogy a jelentésnek az a része, mely közös a jelentés
mindenféle leírásában, és ezért mechanikus következtetési szabályokba foglalható.
Ez a dokumentum a modell-elmélet nevű alapvető technikát használja
egy formális nyelv szemantikájának specifikálására. (Azok az olvasók, akik
kevésbé ismerik a modell-elméletet, haszonnal forgathatják a B. függelékben
szereplő glosszáriumot. Ebben a dokumentumban a
kifejezések előfordulása többnyire egy linket is tartalmaz a kifejezés
glosszáriumban szereplő definíciójára.) A modell-elmélet feltételezi, hogy a
nyelv egy adott 'világ'-ra
hivatkozik, és leírja azokat a minimális feltételeket, amelyeket egy világnak
ki kell elégítenie ahhoz, hogy megfelelő jelentést lehessen rendelni a nyelv
minden kifejezéséhez. Egy adott világot egy interpretációnak hívunk, így tehát a modell-elméletet akár
'interpretáció-elméletnek' is nevezhetnénk. Ennek alapelve az, hogy az ilyen
interpretációk elvárt tulajdonságainak egy olyan absztrakt matematikai
leírását adjuk meg, amelyben a lehető legkevesebb feltételezéssel élünk ezek
tényleges természetére vagy belső struktúrájára nézve, annak érdekében, hogy
az általánosságot a lehető legnagyobb mértékben fenntarthassuk. Egy formális
szemantikai elmélet alapvető célja és szerepe nem az, hogy a nyelv által
leírt dolgok valódi természetének bármiféle mélyebb elemzését adja, vagy hogy
valamilyen konkrét feldolgozási modellt inspiráljon, hanem az, hogy egy
technikai módszert nyújtson annak meghatározásához, hogy mely esetekben érvényes egy következtetési folyamat,
vagyis, hogy mely esetekben őrzi meg az igazságot. Ez lehetővé teszi az
alkalmazások számára a maximális szabadságot, miközben a jelentés általánosan
értelmezett, koherens fogalma is megmarad.
A modell-elmélet tehát megpróbál metafizikai és ontológiai értelemben semleges maradni. Ez
tipikusan a halmazelmélet nyelvén fejezhető ki, egyszerűen azért, mert ez a
matematika normális nyelve – például ez a szemantika feltételezi, hogy
a nevek dolgokat jelölnek egy IR halmazban, amelyet 'univerzum'-nak nevezünk – de a halmazelmélet
nyelvének használata itt koránt sem jelenti azt, hogy az univerzumában lévő
dolgok halmazelméleti természetűek lennének. A modell-elmélet legrelevánsabb
implementációja általában a később leírt következmény fogalmán keresztül valósulhat meg, mely
lehetővé teszi az érvényes következtetés szabályainak
definiálását.
Egy szemantika specifikálásának másik lehetséges módja az, hogy megadnak
egy fordítást az RDF-ről egy formális logikára, kvázi egy hozzá csatolt modell-elmélettel. Ezt az
'axiomatikus szemantikai' közelítést korábban már többen is javasolták és
alkalmazták különböző logikai nyelvekre történő fordításoknál [Conen&Klapsing] [Marchiori&Saarela] [McGuinness&al]. Az RDF és az RDFS
számára is készítettek ilyen fordítást, mely az Lbase
specifikációban [LBASE] van megadva. Az
axiomatikus szemantikai stílusnak van néhány előnye a gépi feldolgozásban, és
olvashatóbb is, ám abban az esetben, ha a választott és alkalmazható
axiomatikus szemantika valamiért nem felelne meg az ebben a dokumentumban
leírt modell-elméleti szemantikának, akkor a modell-elméletet kell
normatívnak tekinteni.
Az RDF-ben a jelentésnek több olyan aspektusa is van, amellyel nem
foglalkozik ez a szemantika; így pl. csupán egyszerű nevekként kezeli az URI
hivatkozásokat, és nem vesz tudomást az egyes URI formákba [lásd: RFC 2396] kódolt jelentések szempontjairól, és
nem nyújt semmiféle elemzést az időben változó adatokról, és az URI
hivatkozásokban beállott változásokról sem. Nem nyújt semmilyen elemzést
továbbá az URI hivatkozások rámutató jellegű használatáról, például egy ilyen
jelentésében, mint 'ez a dokumentum'. Az RDF és RDFS szókészletek
egyes részeihez nem rendel semmilyen formális jelentést, más részeihez pedig
kevesebb jelentést rendel, mint amit elvárhatnánk (ez utóbbira példa a
tárgyiasítási és konténer szókészletek formális kezelése). Ezekre az esetekre
felhívja a figyelmet a dokumentum, és a korlátokat is részletesen ismerteti.
Az RDF egy kijelentéslogika,
amelyben minden egyes triplet egy egyszerű állítást fejez ki. Ez egy meglehetősen szigorú
monotonikus fegyelmet erőltet a
nyelvre, úgy hogy az nem feltételezhet 'zárt világot', és nem fejezhet ki
helyileg alapértelmezett tulajdonságokat, és más, általánosan használt nem-monoton jellegű
konstrukciókat sem.
Az RDF
speciális használata – beleértve azt is, amikor olyan, nagyobb
kifejező erejű nyelvek bázisaként alkalmazzuk, mint a DAML+OIL [DAML] és OWL [OWL] – további szemantikai feltételekkel
gyarapíthatja az eddig leírtakat, és az ilyen extra szemantikai feltételek
befolyásolhatják az egyes RDF szókészletek kifejezéseinek jelentését is. Az RDF
kiterjesztéseit vagy dialektusait, amelyekhez az ilyen extra szemantikai
feltételek bevezetése útján jutunk, az RDF szemantikai
kiterjesztéseinek is nevezhetjük. Az RDF szemantikai kiterjesztéseinek
korlátait ebben az ajánlásban az [RFC
2119] szabvány által definiált ilyen kulcsszavakkal korlátozzuk
mint MUST,
MUST
NOT, SHOULD és MAY [és ezeket az angol kifejezéseket a magyar
fordításban is (zárójelben) kiírjuk, hogy a korlátok szabványos jelentése
garantálható legyen a magyar nyelv hasonló szavainak némileg eltérő jelentése
ellenére is – a ford.] Az RDF szemantikai kiterjesztéseinek meg
kell felelniük (MUST conform) az egyszerű
interpretációkra megadott szemantikai feltételeknek, amelyeket az 1.3 az 1.4, és az 1.5 szekció ismertet, valamint az RDF interpretációkra
megadott azon feltételeknek, amelyeket e dokumentum 3.1
szekciója ír le. Egy szemantikai kiterjesztésben minden
következmény-nevet egy szókészlet-következmény kifejezéssel kell
megjelölni (SHOULD be indicated). Egy RDF
szemantikai kiterjesztésre megadott szemantikai feltételeknek definiálniuk
kell (MUST
define) egy szókészlet-következmény fogalmat, mely érvényes a szerint a modell-elméleti szemantika
szerint, amelyet a jelen dokumentum normatív részei írnak le; ez alól
kivétel, ha a szemantikai kiterjesztés a gráfok valamilyen szintaktikailag
korlátozott részhalmazára van definiálva – ilyenkor a szemantikai
feltételeket csak erre a részhalmazra kell alkalmazni. Az ilyen,
szintaktikailag korlátozott szemantikai kiterjesztések specifikációinak
tartalmazniuk kell (MUST include) a szintaktikai
feltételeik olyan specifikációját, mely elegendő ahhoz, hogy egy szoftver
képes legyen egyértelműen megkülönböztetni azokat az RDF gráfokat, amelyekre érvényesek a szemantikai
feltételek, azoktól, amelyekre nem. Azok az alkalmazások, amelyek az ilyen,
szintaktikailag korlátozott szemantikai kiterjesztésekre épülnek,
szintaktikai hibaként kezelhetik (MAY treat) azokat az RDF gráfokat, amelyek nem felelnek meg
az előírt szintaktikai korlátozásoknak.
Az RDF szemantikai kiterjesztésére példa az RDF Séma [RDF-SZÓKÉSZLET], amelyet RDFS-ként
rövidítünk, és amelynek szemantikáját e dokumentum későbbi fejezeteiben
definiáljuk. Az RDF Séma nem ír elő extra szintaktikai korlátozásokat.
Minden szemantikai elméletet valamilyen szintaxishoz kell kapcsolni. Az
RDF szemantikáját az RDF absztrakt
szintaxisához kapcsolva definiáljuk, amelyet "Az RDF alapfogalmai és
absztrakt szintaxisa" című [RDF-FOGALMAK] dokumentum ír le. Ez a
dokumentum a következő terminológiát használja: URI
hivatkozás, literál,
típus
nélküli literál, tipizált
literál, XML-literál,
XML
érték, csomópont,
üres
csomópont, triplet
és RDF
gráf. A jelen dokumentumban végig, amikor a 'karakterlánc'
fogalmát használjuk, mindig egy Unicode karaktersorozatra és a hozzá tartozó
'nyelv teg'-re gondolunk (az RFC 3066 szabvány értelmében. – Vö. az
[RDF-FOGALMAK] dokumentum 6.5
szekciójával). Jegyezzük meg, hogy az RDF gráf karakterláncainak Normal
Form C kódolásban kell lenniük (SHOULD be).
Ez a dokumentum az RDF gráfok
leírására a triplet notációs (N-Triples) szintaxist
használja, amelyet "Az RDF tesztsorozata" című [RDF-TESZTEK] dokumentum definiál. Ez a
notáció az ürescsomópont-azonosító
(nodeID) konvenciót használja a gráf tripletjeiben az üres csomópontok
jelölésére. Noha az ilyen csomópont
azonosítók, mint '_:xxx', üres csomópontok azonosítására
szolgálnak a felületi szintaxisban, mégsem tekinthetők az adott gráfcsomópont
címkéjének; ezek ugyanis nem nevek, és nem részei a tényleges gráfnak. Sőt,
két RDF gráf, amelyet két olyan N-Triples szintaxisú
dokumentum ír le, amelyek csupán az üres csomópontjaik
átnevezése miatt térnek el egymástól, egyenértékű
gráfoknak tekintendők. Ezt az
átnevezési konvenciót úgy kell érteni, hogy mindig egész dokumentumra
vonatkozik, mert ha a csomópontokat csupán a dokumentum egy részében nevezzük
át, akkor ez olyan dokumentumot eredményezhet, mely már egy különböző RDF gráfot ír le.
Az N-Triples szintaxis elvárja, hogy az URI hivatkozásokat teljes hosszban
kiírjuk, és hegyes zárójelek közé tegyük. A rövidítés kedvéért az
illusztratív példákban az 'ex:' típusú képzetes URI sémát használjuk. Hogy az
olvasó realisztikusabb képet kapjon az N-Triples szintaxisról, képzeljen az
'ex:' helyére valami ilyen karakterláncot:
http://www.example.org/rdf/mt/artificial-example/. A
konvencionális rdf:, rdfs: és xsd: minősített-név
(QName) prefixek definíciója az alábbi:
Prefix = rdf:, névtér-URI =
http://www.w3.org/1999/02/22-rdf-syntax-ns#
Prefix = rdfs:, névtér-URI =
http://www.w3.org/2000/01/rdf-schema#
Prefix = xsd: névtér-URI =
http://www.w3.org/2001/XMLSchema#
Minthogy a QName szintaxis használata nem legális az N-Triples
szintaxisban, de a rövidség és a könnyebb olvashatóság érdekében mégis
használni szeretnénk, a példáinkban azt a konvenciót követjük, hogy a
minősített neveket (QNames) hegyes zárójelek nélkül írjuk, és ezeket úgy
tekintjük, mintha a nekik megfelelő URI hivatkozásokat írnánk le hegyes
zárójelek között. Például az alábbi triplet:
<ex:a> rdf:type rdfs:Class .
úgy olvasandó, mintha N-Triples szintaxissal ezt írtuk volna le:
<ex:a> <http://www.w3.org/1999/02/22-rdf-syntax-ns#type>
<http://www.w3.org/2000/01/rdf-schema#Class> .
Az általános szemantikai feltételek ismertetésénél használt
névkonvencióban az egyedül álló karaktereket, vagy az olyan
karaktersorozatokat, amelyekben nem szerepel kettőspont, tetszőleges
neveknek, üres csomópontoknak, vagy karakterláncoknak stb. tekintjük. A
konkrét jelentést az adott kontextus specifikálja.
Egy RDF
gráf, vagy egyszerűen csak gráf, RDF tripletek
halmaza.
Egy RDF gráf részgráfja a gráfot
alkotó tripletek részhalmaza. Egy tripletet az őt ábrázoló elemi gráffal
azonosítunk úgy, hogy a gráf minden egyes tripletjét egy-egy részgráfnak
(subgraph) tekintjük. Egy valódi részgráf a gráfban szereplő
tripletek valódi részhalmaza.
Egy RDF alapgráf olyan gráf, amelynek
nincs üres csomópontja.
Egy név egy URI hivatkozás, vagy
egy literál. Ezek azok a kifejezések, amelyekhez jelentést kell
kapcsolnunk egy interpretáció révén. Megjegyzendő, hogy egy
tipizált literál két névből áll: önmagából és a típusát jelző, belső URI
hivatkozásból.
A nevek halmazát szókészletnek nevezzük. Egy
gráfnak a szókészlete olyan nevek halmaza, amelyek a gráf valamelyik
tripletjében előforduló alanyt, állítmányt vagy tárgyat azonosítják.
Megjegyezzük, hogy azoknak az URI hivatkozásoknak, amelyek csak tipizált
literálokban fordulnak elő, nem szükséges a gráf szókészletében lenniük.
Tételezzük fel, hogy M egy leképezés egy
ürescsomópont-halmazról literálok, üres csomópontok és URI hivatkozások
valamilyen halmazára; ekkor bármilyen gráf, amelyet úgy nyerünk egy G
gráfból, hogy annak néhány, vagy összes N üres csomópontját egy M(N)
leképezéssel helyettesítjük, G egyik példánya lesz.
Megjegyzendő, hogy minden gráf egyben példánya is önmagának, továbbá hogy G
valamelyik példányának a példánya szintén G egyik példánya, valamint, ha
G-nek egy példánya H, akkor H minden tripletje egyben G valamelyik
tripletjének a példánya is.
Egy V szókészletre
vonatkozó példány egy olyan példány, amelyben az összes név, amellyel az eredeti gráf üres csomópontjait
helyettesítettük, a V szókészletből való.
Egy gráf valódi példánya
(proper instance) egy olyan példány, amelyben egy üres csomópontot egy névvel
helyettesítettünk, vagy pedig a gráf két üres csomópontját a példány azonos
csomópontjára képeztük le.
Egy gráf bármilyen példánya, amelyben egy üres csomópontot egy olyan új
üres csomópontra képeztünk le, mely nem szerepelt az eredeti gráfban, az
eredetinek a példánya, az eredeti pedig emennek a példánya, és ez a folyamat
ismételhető, úgy hogy bármilyen 1:1 arányú leképezés az üres csomópontok
között a gráfnak egy olyan példányát definiálja, amelynek viszont az eredeti
gráf a példánya. Azt a két gráfot, amelyek egymás példányai, de egyikük sem
valódi példány (vagyis, csak az üres csomópontjaik identitásában
különböznek egymástól), egyenértékű
gráfoknak tekintjük. Két egyenértékű gráfot azonos gráfként fogunk kezelni.
Ez lehetővé teszi számunkra, hogy elkerüljünk néhány olyan problémát, amelyek
az ürescsomópont-azonosítók (nodeID) ''átnevezéséből' keletkeznek, ráadásul
ez megfelel annak a konvenciónak
is, hogy az üres csomópontoknak nincs címkéjük. Az egyenértékű gráfok
kölcsönös példányok, invertálható példányleképezéssel.
Egy RDF gráfról azt mondjuk, hogy
"sovány", ha nincs egyetlen olyan példánya sem, mely valódi
részgráfja lenne a gráfnak. A nem-sovány gráfok rendelkeznek
bizonyos belső redundanciával, és ugyanazt a tartalmat fejezik ki, mint a
sovány részgráfjuk. Például az alábbi gráf:
<ex:a> <ex:p> _:x .
_:y <ex:p> _:x .
nem sovány, az
<ex:a> <ex:p> _:x .
_:x <ex:p> _:x .
azonban sovány.
RDF gráfok egy halmazának
egyesítését a következőképpen definiáljuk: Ha a halmazban lévő
gráfoknak nincs közös üres csomópontjuk, akkor a gráfok uniója lesz az
egyesítés. Ha van közös üres csomópontjuk, akkor az egyesítést azon gráfok
uniója alkotja, amelyekhez úgy jutunk, hogy olyan (egyenértékű) gráfokkal
helyettesítjük őket, amelyeknek nincsenek közös üres csomópontjaik. Ezt az
eljárást gyakran úgy emlegetjük, hogy az üres csomópontokat
'szétszabványosítottuk'. Könnyen belátható, hogy bármelyik két egyesítés
egyenértékű, így tehát az egyesítésről beszélünk, követve az
egyenértékű gráfok konvencióját. Alkalmazva az egyenértékű gráfok és az
egyenértékű identitás konvencióját, az eredeti halmazban lévő bármilyen
gráfot az egyesítés részgráfjának tekintünk.
Általában nem juthatunk egy gráfhalmaz egyesítéséhez oly módon, hogy
egybetoldjuk a nekik megfelelő N-Triples formátumú
dokumentumokat, és felépítjük az így egyesített dokumentum által leírt
gráfot. Ha a dokumentumok közül néhány ugyanazokat a csomópont-azonosítókat
használja, akkor az egyesített dokumentum egy olyan gráfot ír le, amelyben
néhány üres csomópont azonosítása 'véletlenszerű' lesz. Ahhoz, hogy N-Triples dokumentumokat
egyesíthessünk, ellenőriznünk kell, hogy nem használja-e két vagy több
dokumentum ugyanazt az azonosítót (nodeID), és ha igen, akkor mindegyiket ki
kell cserélnünk valami különbözőre, mielőtt egyesítjük a dokumentumokat.
Ugyanilyen elővigyázatosságra van szükség a gráfok egyesítésénél akkor is, ha
olyan RDF/XML dokumentumok írják le őket, amelyekben ürescsomópont-azonosítók
vannak. (Lásd Az RDF/XML
szintaxis specifikációja (átdolgozott kiadás) [RDF-SZINTAXIS] dokumentumban.)
Az RDF nem ír elő semmilyen logikai korlátozást a tulajdonságok
érvényességi körére és értéktartományára, s így különösen nem akadályozza
meg, hogy egy tulajdonságot önmagára alkalmazzunk. Továbbá, amikor osztályokat vezetünk be RDFS-ben, azok
tartalmazhatják önmagukat is. Úgy tűnhet, hogy az ilyen 'tagsági hurkok'
megsértik a fundáltság axiómát, a Zermelo-Fraenkel-féle halmazelmélet egyik
axiómáját (axiom of foundation), mely tiltja a tagságok vég nélküli leszálló
láncolatát. A jelen dokumentumban megadott szemantikai modell azonban
különbséget tesz a tulajdonságok és osztályok mint objektumok, illetve ezek
kiterjedése – vagyis azon
objektum-érték párok halmaza, amelyek kielégítik a tulajdonságot, vagy azon
dolgok halmaza, amelyek az osztályban 'vannak' – között, lehetővé
téve ezáltal, hogy egy tulajdonság vagy osztály kiterjedése tartalmazza a
tulajdonságot vagy az osztályt, magát is, anélkül, hogy ezzel megsértenénk a
fundáltság axiómát. Különösen fontos, hogy az osztálykiterjedés-leképezés
ilyen használata lehetővé teszi az osztályoknak, hogy önmagukat tartalmazzák.
Például teljesen helyénvaló, hogy egy 'univerzális' osztály (kiterjedése)
tartalmazza az osztályt, mint tagot, ami egy gyakran alkalmazott konvenció az
osztályhierarchia csúcsán. (Ha azonban az osztály kiterjedése úgy tartalmazná
önmagát, mint saját kiterjedését, akkor az axióma valóban sérülne,
de ez a helyzet a mi esetünkben sohasem áll elő.) Ennek technikáját
teljességében tárgyalja [Hayes&Menzel].
Ebben a tekintetben az RDFS különbözik sok konvencionális ontológiai
keretrendszertől (mint pl. az UML), amelyek az egyedek egy strukturáltabb
hierarchiáját feltételezik (egyedek halmazait stb.), vagy amelyek egy szigorú
választóvonalat húznak az adatok és a meta-adatok közé. Az RDFS nem
feltételezi ugyan ilyen struktúrák létezését, de nem is zárja ki. Az RDF
lehetővé teszi a tagsági hurkokat, de nem teszi kötelezővé ezek használatát
egy felhasználói szókészlet minden részében. Ha az RDFS-nek ez az aspektusa
aggasztónak tűnik, akkor ez a lehetőség esetleg korlátozható az RDF gráfok
egy olyan részhalmazára, mely nem tartalmaz ilyen osztálytagsági vagy
tulajdonságalkalmazási 'hurkot'; ettől függetlenül megmaradhat az RDFS
kifejező erejének nagy része, mely sok gyakorlati célra alkalmassá teszi;
emellett az ilyen szemantikai kiterjesztések szintaktikai feltételeket is
kiköthetnek, amelyek eleve megtilthatják az ilyen hurkolt konstrukciókat.
Az explicit kiterjedés-leképezés használata lehetővé teszi, hogy két
tulajdonság pontosan ugyanazokkal az értékkel rendelkezzék, vagy hogy két
osztály ugyanazokat az egyedeket tartalmazza, és mégis különböző entitások
maradjanak. Ez azt jelenti, hogy az RDFS osztályokat jóval többnek kell
tekintenünk, mint egyszerű halmazoknak; Ezeket 'osztályozásoknak' vagy
'fogalmaknak' tekinthetjük, amelyek sokkal erőteljesebb fogalmi identitással
rendelkeznek, mint az egyszerű extenzionális azonosság. A modell-elméletnek ez a tulajdonsága jelentős
következményekkel jár az olyan, nagyobb kifejező erejű nyelvekre, amelyek az
RDF-re épülnek, mint pl. az OWL [OWL],
mely így közvetlenül képes kifejezni az azonosságot osztályok és
tulajdonságok között. Az osztályoknak és tulajdonságoknak erről az 'intenzionális' természetéről
néha azt állítják, hogy fontos tulajdonság egy leíró nyelv esetében, de ennek
a kérdésnek a kimerítő tárgyalása meghaladja e dokumentum kereteit.
Vegyük észre azonban, hogy az a kérdés, hogy egy osztály tartalmazza-e
önmagát tagként, teljesen különbözik attól a kérdéstől, hogy alosztálya-e
önmagának, vagy sem. Minden osztály egyértelműen alosztálya is önmagának.
Azok az olvasók, akik jól ismerik a konvencionális logikai szemantikát,
hasznosnak találhatják úgy felfogni az RDF-et, mint az egzisztenciális binér
relációs logika egy változatát, amelyben a relációk első osztályú entitások a
kvantifikáció univerzumában. Egy ilyen logikához juthatunk az R(a,b) relációs
atomnak egy konvencionális logikai szintaxisba történő bekódolásával, ha
használunk egy képzeletbeli Triplet(a,R,b) relációt; az itt leírt alapvető
szemantika rekonstruálható ebből a szemléletből az y kiterjedésének egy ilyen
halmazként történő definiálásával: {<x,z> : Triplet(x,y,z)}, valamint
annak megjegyzésével, hogy pontosan ez lenne R jelentése a konvencionális
Tarski-féle modell-elmélet relációs atomjának eredeti, R(a,b) formájában.
Ugyanez a konstrukció követhető nyomon az Lbase axiomatikus leírás
[LBASE] szemantikájában is.
Ez a dokumentum nem foglal állást azzal kapcsolatban, hogy az URI
hivatkozások komponálhatók-e más kifejezésekből, pl. relatív URI-kből vagy
minősített nevekből (QName); a szemantika egyszerűen feltételezi, hogy az
ilyen lexikális kérdések már meg vannak oldva valamilyen globálisan koherens
módon, tehát úgy tekinthető, hogy egy adott URI hivatkozás mindig ugyanazt
jelenti, bárhol jelenjék is meg. Hasonlóképpen, a szemantika nincs
felkészítve arra sem, hogy nyomon kövesse az időbeni változásokat, hanem
implicit módon feltételezi, hogy az URI hivatkozások mindig ugyanazt
jelentik, bármikor használják őket. Egy olyan adekvát szemantika
létrehozása, amelyik érzékeny lenne a temporális változásokra, már egy olyan
kutatási probléma, mely kívül esik ennek a dokumentumnak a tárgykörén.
A szemantika nem feltételez semmilyen speciális viszonyt egy URI
hivatkozás jelentése, és a között a webes vagy másféle erőforrás között,
amely ezzel az URI hivatkozással elérhető akár HTTP protokollon keresztül,
akár más módon. Egy ilyen igény teljesíthető esetleg egy szemantikai
bővítménnyel, mert az itt leírt formális szemantika nem feltételez semmilyen
kapcsolatot az URI hivatkozások elnevezése és az ilyen hivatkozások más
protokollban történő használata között.
A szemantika minden RDF nevet
csupán egy olyan kifejezésnek tekint, ami valamit jelent. Az ilyen "valamit"
itt 'erőforrásnak' nevezzük az [RFC
2396] szabvány szerint, de ez a szemantika semmilyen
feltételezéssel nem él az erőforrások természetére nézve; az 'erőforrást'
csupán úgy kezeli, mintha az 'entitás' szinonimája volna, vagyis, egy olyan
általános fogalom, amibe bármi belefér az adott univerzumon belül.
A nevek különböző szintaktikai
formáit egyedi módon kezeljük. Az URI hivatkozásokat egyszerűen csak logikai
konstansoknak tekintjük. A típus nélküli literálokat úgy tekintjük, hogy
önmagukat jelentik, s így rögzített jelentésük van. A tipizált literálok
jelentése egy olyan érték, amely a benne lévő karakterláncnak a benne
megjelölt típus szerinti leképezése. Az RDF egy speciális jelentést kapcsol
azokhoz a literálokhoz, amelyek rdf:XMLLiteral-ként vannak
tipizálva (lásd a 3. szekcióban
ennek a leírását.
A modell-elméleti szemantika alapvető belső szemlélete az, hogy egy mondat
kimondása nem más, mint egy tényállítás a világról: egyfajta kifejezése
annak, hogy a világ valójában úgy van elrendezve, mint egy olyan
interpretáció, mely igazzá teszi ezt a mondatot. Más szóval: egy tényállítás
egyenértékű egy korlátozás kimondásával arról, hogy milyen
lehet a világ. Vegyük észre, azonban, hogy itt nincs olyan
feltételezés, hogy egy tényállítás elegendő információt tartalmaz ahhoz, hogy
egyetlen kizárólagos interpretációt specifikáljon. Általában is lehetetlen
elegendő tényállítást tenni bármilyen nyelven ahhoz, hogy egyetlen lehetséges
világra korlátozzuk az interpretációt, így tehát nem létezik efféle fogalom
sem, hogy "egy RDF gráf kizárólagos interpretációja". Általában
minél nagyobb egy RDF gráf – azaz, minél többet jelent ki a világról,
annál kisebb lesz az interpretációknak az a halmaza, amelyet a gráf egy tényállítása igazzá tehet –
annál kevesebb olyan elrendezése lehet a világnak, mely igazzá teszi a
gráfot.
Az interpretáció alábbi definícióját a matematika nyelvén fejezzük ki, és
amit ez szemléleti értelemben jelent, az annyi, hogy egy interpretáció éppen
elegendő információt nyújt a világ egy lehetséges elrendezéséről – egy
'lehetséges világról' – ahhoz, hogy egy RDF alapgráf bármelyik tripletjének igazságértékét (igaz vagy
hamis voltát) meg lehessen állapítani. Az interpretáció ezt oly módon teszi,
hogy minden URI hivatkozás számára specifikálja, hogy az minek a neve, hogy
mit jelöl, és ha ez egy tulajdonságot jelöl, akkor annak milyen értékei
vannak az adott univerzumban
lévő minden egyes dolog számára; ha pedig ez egy adattípust jelöl, akkor specifikálja a leképezést az
adat lexikális formája és értéke között. Ez éppen elegendő információ ahhoz,
hogy megállapíthassuk egy alapgráf
tripletjének, és így magának a teljes alapgráfnak is az igazságértékét. (A
nem-alapgráfokat a következő szekcióban tárgyaljuk.) Jegyezzük meg, hogy ha
ezek közül az információk közül bármelyiket kihagynánk, akkor előfordulhatna,
hogy egyes jól formált
tripletek határozott igazságérték nélkül maradnának; továbbá, hogy minden más
információ is, mint pl. az univerzumban lévő dolgok egzakt természete –
tekintet nélkül annak belső érdekére – irreleváns lenne bármelyik
triplet tényleges igazságértéke szempontjából.
Minden interpretációt nevek egy
halmazához viszonyítunk, amelyet az interpretáció szókészletének nevezünk; az
interpretációról tehát, szigorúan véve, azt mondhatjuk, hogy az mindig egy
RDF szókészlet interpretációja, és nem magáé az RDF-é. Egyes interpretációk
speciális jelentéseket rendelhetnek egy adott szókészlet szimbólumaihoz. Azok
az interpretációk, amelyek számára közös egy adott szókészlet speciális
jelentése, erről a szókészletről vannak elnevezve (pl. rdf-interpretatáció, rdfs-interpretáció stb). Az olyan interpretációt,
amelynek nincsenek konkrét extra feltételei egy szókészletre (beleértve magát
az RDF szókészletet is), egyszerű interpretációnak, vagy csak
interpretációnak hívjuk.
Az RDF a literálok több formáját használja. A literálok legfőbb
szemantikai jellemzője, hogy az értéküket nagymértékben meghatározza annak a
karakterláncnak a formája, amelyet tartalmaznak. A típus nélküli literálokat
(amelyek nem tartalmaznak URI hivatkozást), mindig úgy értelmezzük, hogy
önmagukra hivatkoznak, legyenek azok akár egyszerű karakterláncok, akár olyan
párosok, amelyek egy karakterláncból és egy nyelv-tegből
állnak; az ilyen karakterláncra minkét esetben úgy hivatkozunk, hogy "leterál
karakterlánc". A tipizált literálok esetén azonban a jelentés teljes
meghatározása attól függ, hogy hozzáférhetünk-e valamilyen
adattípus-információhoz, ami csak az RDF-en kívül érhető el. A tipizált
literálok jelentésének komplett diszkussziója az 5.
fejezetben található, mely bevezeti az adattípus interpretáció
speciális fogalmát. Minden interpretáció egy IL leképezést definiál tipizált
literálokról ezek interpretációira. Az IL-re vonatkozóan egyre erősebb
feltételeket definiálunk, ahogy az 'interpretáció' fogalmat fokozatosan
kiterjesztjük a későbbi szekciókban.
Ebben a dokumentumban végig, precíz szemantikai feltételeket adunk meg
táblázatos formában; ezek között lesznek olyan táblázatok, amelyek
szemantikai feltételeket állapítanak meg, továbbá olyan táblázatok, amelyek
igaz állításokat és érvényes
következtetési szabályokat tartalmaznak, és olyan táblázatok is, amelyek a
szintaxist listázzák ki; ezeket a táblázatokat más-más háttérszínnel
különböztetjük meg. Ezeknek a táblázatoknak az együttese az egész szemantika
formális összefoglalását adja meg. Jegyezzük meg, hogy az RDF szemantikája
nem függ az RDFS szemantikájától. Az RDF teljes szemantikáját az 1. és a 3. fejezet, az RDFS
teljes szemantikáját pedig az 1.,a 3. és a 4. fejezet
definiálja.
Egy egyszerű interpretáció definíciója
Egy V szókészlet egyszerű I
interpretációját az alábbiak definiálják:
1. Erőforrások egy nem üres IR halmaza, amelyet I értelmezési
tartományának, vagy univerzumának nevezünk.
2. Egy IP halmaz, amely I tulajdonságainak a
halmaza.
3. Egy IEXT leképezés I-ről az IR x IR hatványhalmazra (azaz olyan
<x,y> párok halmazának a halmazára, ahol x és y az IR
elemei).
4. Egy IS leképezés a V-ben szereplő URI hivatkozásokról az IR és
IP uniójára.
5. Egy IL leképezés a V-ben szereplő tipizált literálokról
IR-re.
6. Az IR halmaznak egy megkülönböztetett LV részhalmaza, mely V
összes típus nélküli literáljának a halmaza.
|
Az IEXT(x), az x kiterjedése (extenziója), azon párok halmaza,
amelyek azokat az argumentumokat azonosítják, amelyekre a tulajdonság igaz,
vagyis, ez az x binér relációs kiterjedése. Az a trükk hogy megkülönböztetjük
a relációt mint objektumot a relációs kiterjedésétől, lehetővé teszi, hogy
egy tulajdonság saját kiterjedésében is előfordulhasson, amint azt fentebb már tárgyaltuk.
Az a feltételezés, hogy LV az IR részhalmaza, ugyanazt jelenti, mintha azt
mondanánk, hogy a literál-értékeket valódi, 'létező' entitásoknak tekintjük,
ez pedig azzal a kijelentéssel egyenértékű, hogy a literál értékek
erőforrások. Ez azonban nem implikálja azt, hogy a literálokat URI
hivatkozásokkal kellene azonosítanunk. Megjegyezzük , hogy az LV halmaz a
típus nélküli literálok mellett tartalmazhat más elemeket is. Technikai okai
vannak annak, hogy IL értéktartománya miért IR, és hogy miért nem
korlátozódik csupán LV-re. Amikor az interpretációk figyelembe veszik az adattípus információt,
szintaktikailag lehetséges, hogy egy tipizált literál belülről inkonzisztens
legyen, és az ilyen, rosszul tipizált literáloknak nem-literál
(non-literal) értéket kell megjelölniük, ahogy az 5. fejezet magyarázza.
A következő szekciók azt definiálják, hogy egy szókészlet interpretációja
miként határozza meg egy RDF gráf igazságértékeit, az RDF kifejezések
jelentésének (szemantikai "értékének") rekurzív definíciójával, mely a
kifejezések közvetlen alkifejezéseinek jelentéseire épül. Ez érvényes minden
további szemantikai kiterjesztésre is. Az RDF-nek kétféle jelentéshordozója
van: a nevek jelentik a dolgokat az
univerzumban, a tripletek halmazai pedig igazságértékeket jelentenek.
Egy RDF alapgráf jelentése I-ben rekurzív módon van
megadva az alábbi szabályok segítségével, amelyek kiterjesztik az
I interpretációs leképezést nevekről alapgráfokra. Ezek a szabályok (és a később
ismertetendő kiterjesztéseik) úgy működnek, hogy egy E RDF
szintaxis bármely szakaszának jelentését E közvetlen
szintaktikai összetevőinek jelentéseivel definiálják, lehetővé téve, ily
módon, bármilyen RDF kódszekció jelentésének egyfajta szintaktikai
rekurzióval történő meghatározását.
Az alábbi táblázatban, és végig ebben a dokumentumban az egyenlőségjel (=)
azonosságot jelent, az ilyen hegyes zárójeles kifejezések, mint (<x,y>)
pedig az x-ből és y-ból álló rendezett párt ábrázolják. Az RDF gráfszintaxist
az N-Triples nevű
triplet notációs konvenció használatával jelezzük, ahogyan ezt "Az RDF
tesztsorozata" dokumentum [RDF-TESZTEK] leírja: a literál
karakterláncok idézőjelek között szerepelnek, a nyelv tegeket '@' karakterek
jelzik, a tripleteket pedig pont karakterek (.) zárják.
Szemantikai feltételek az alapgráfokra
| Ha E egy "aaa" típus
nélküli literál V-ben, akkor I(E) = aaa |
| Ha E egy "aaa"@ttt
típus nélküli literál V-ben, akkor I(E) = <aaa,
ttt> |
| Ha E egy tipizált literál
V-ben, akkor I(E) = IL(E) |
| Ha E egy URI hivatkozás
V-ben, akkor I(E) = IS(E) |
Ha E egy s p o .
alapgráf-triplet, akkor I(E) = igaz, ha
s, p és o eleme V-nek, I(p)
eleme IP-nek és <I(s),I(o)>
eleme IEXT(I(p))-nek,
egyébként I(E) = hamis.
|
| Ha E egy RDF alapgráf,
akkor I(E) = hamis, ha I(E') = hamis valamely
E-ben lévő E' triplet számára, egyébként I(E) =
igaz. |
Ha egy RDF gráf szókészlete olyan neveket tartalmaz, amelyek nem
szerepelnek egy I interpretáció szókészletében – azaz, ha I egyszerűen
nem ad szemantikai értéket egy olyan névnek, amelyik szerepel a gráfban – akkor ezek az
igazságfeltételek mindig a "hamis" értéket adják valamelyik tripletnek a
gráfban, és ezáltal magának a gráfnak is. Megfordítva ez azt jelenti, hogy a
gráf minden tényállítása implicite azt is kimondja, hogy a gráfban minden név ténylegesen hivatkozik valamire a
világban. A táblázatban lévő utolsó feltétel implikálja, hogy egy üres gráf
(a tripletek üres halmaza) triviálisan "igaz" értékű.
Figyeljük meg, hogy a típus nélküli literálok jelentése mindig benne van
LV-ben, bármelyik igaz triplet alanyának és tárgyának jelentése pedig benne
van IR-ben. Így bármelyik URI hivatkozás, amelyik előfordul egy gráfban, akár
állítmányként, akár pedig alanyként vagy tárgyként, jelentenie kell valamit
az IP és IR halmazok metszetében, bármely interpretációban, amelyik kielégíti
a gráfot.
Illusztratív példaként megadunk egy kisebb interpretációt a következő
"mesterkélt" szókészletre {ex:a, ex:b,
ex:c, "bármi", "bármi"^^ex:b}. Egész
számokat használunk a nem-literális dolgok ('things') jelölésére az
univerzumban. Ez nem akarja azt jelenteni, hogy az interpretációkat úgy
értelmezzük, hogy aritmetikáról szólnak, hanem inkább azt kívánja
hangsúlyozni, hogy az univerzumban lévő dolgok egzakt természete irreleváns.
Az LV bármilyen halmaz lehet, ami kielégíti a szemantikai feltételeket.
(Ebben, és a következő példákban is a "<" és a ">" szimbólumokat
különböző módokon használjuk: a matematikai használatot követve absztrakt
párokat és N-eseket jelölnek, az N-Triples szintaxisban pedig URI
hivatkozásokat zárnak közre. Emellett nyílhegyként is előfordulhatnak, és
ilyenkor leképezést szimbolizálnak.)
IR = LV union{1, 2}
IP={1}
IEXT: 1=>{<1,2>,<2,1>}
IS: ex:a=>1, ex:b=>1,
ex:c=>2
IL: "bármi"^^ex:b =>2
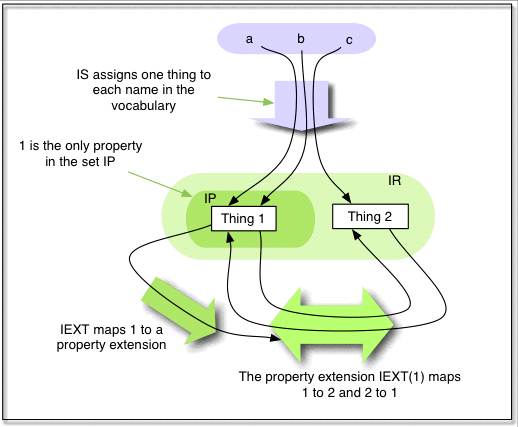
1. példa: Egy interpretációs példa.
Megjegyzés: Ez nem egy RDF gráf képe. (Az ábra nem tünteti fel, hogy az LV
halmaz elemeinek száma végtelen.)
Az ábrán lévő feliratok magyar fordítása felülről lefelé:
IS hozzárendel egy-egy dolgot minden névhez a szókészletben.
1 az egyetlen tulajdonság az IP halmazban.
IEXT leképezi 1-et egy tulajdonság-kiterjedésre.
Az IEXT(1) tulajdonság-kiterjedés 1-et leképezi 2-re, 2-t pedig 1-re.
Ez az interpretáció az alábbi tripleteket igazzá teszi:
<ex:a> <ex:b> <ex:c> .
<ex:c> <ex:a> <ex:a> .
<ex:c> <ex:b> <ex:a> .
<ex:a> <ex:b> "bármi"^^<ex:b>
.
Például, I(<ex:a> <ex:b> <ex:c> .) = igaz
ha <I(ex:a),I(ex:c)> eleme
IEXT(I(<ex:b>))-nek, azaz, ha <1,2> benne van
IEXT(1)-ben, ami {<1,2>,<2,1>} és így valóban tartalmazza
<1,2>-t, tehát I(<ex:a <ex:b> ex:c>) =
igaz.
A negyedik triplet igazságértéke annak a meglehetősen sajátos
interpretációnak a következménye, amelyet itt a tipizált literálok számára
választottunk.
Ebben az interpretációban IP az IR részhalmaza; ez jellemző lesz az RDF
további szemantikai interpretációira is, de ez nem követelmény.
Ez az interpretáció a következő tripleteket hamissá teszi:
<ex:a> <ex:c> <ex:b> .
<ex:a> <ex:b> <ex:b> .
<ex:c> <ex:a> <ex:c> .
<ex:a> <ex:b> "bármi" .
Például, I(<ex:a> <ex:c> <ex:b> .) = igaz,
ha <I(ex:a), I(<ex:b>)>, azaz
<1,1>, eleme IEXT(I(ex:c))-nek; de I(ex:c)=2,
ami nincs benne IP-ben, így IEXT nincs definiálva 2-re, ezért a feltétel nem
teljesül, tehát I(<ex:a> <ex:c> <ex:b> .) =
hamis.
Ez hamissá teszi az összes olyan tripletet is, amelyik típus nélküli
literált tartalmaz, mivel a tulajdonság-kiterjedésben nincs egyetlen olyan
pár sem, amelyik egy típus nélküli literált tartalmazna.
Hangsúlyozzuk: ez csak egy lehetséges interpretációja ennek a
szókészletnek; elképzelhető (végtelenül) sok más is. Például, ha ezt az
interpretációt úgy módosítanánk, hogy a tulajdonság-kiterjedést az 1 helyett
a 2-höz csatolnánk, akkor a fenti tripletek közül egyik sem lenne "igaz".
Ez a példa illusztrálta, hogy bármilyen interpretáció, mely leképez egy
állítmány szerepű URI hivatkozást valamire, ami nincs benne az IP-ben, az
hamissá teszi a gráfot.
Az üres csomópontokat úgy kezeljük, hogy ezek egyszerűen csak jelzik
valamilyen dolognak a létezését anélkül, hogy használnánk ennek a dolognak a
nevét, vagy bármit mondanánk a nevéről. (Ez nem ugyanaz, mintha azt
feltételeznénk, hogy egy üres csomópont egy 'ismeretlen' URI hivatkozást
jelöl; például, ez nem feltételezi, hogy létezik bármiféle URI hivatkozás,
ami erre a dologra hivatkozik. A Skolemizácó diszkussziója, mely az A. függelékben található, releváns erre az esetre.)
Egy interpretáció specifikálhatja egy olyan gráf igazságértékét, amelyik
üres csomópontokat tartalmaz. Ehhez szükség lesz néhány definícióra, minthogy
az elmélet eddig még nem adott semmilyen jelentést az üres csomópontoknak.
Tegyük fel, hogy I egy interpretáció, és A egy leképezés üres csomópontok
valamely halmazáról I-nek az IR univerzumára, és definiáljuk, hogy I+A legyen
egy kiterjesztett interpretáció, mely olyan, mint I, azzal a különbséggel,
hogy itt A-t használjuk arra, hogy megadja az üres csomópontok
interpretációját. Definiáljuk üres(E)-t mint az E-ben lévő üres csomópontok
halmazát. Ezután a fenti szabályok kiterjeszthetők úgy, hogy tartalmazzák azt
a két új esetet, amelyeket akkor vezetünk be, amikor üres csomópontok
fordulnak elő a gráfban:
Szemantikai feltételek üres csomópontokra
| Ha E egy üres csomópont, és
A(E) definiálva van, akkor [I+A](E) = A(E) |
| Ha E egy RDF gráf, akkor
I(E) = igaz, ha [I+A'](E) = igaz valamely A',
üres(E)-ről IR-re történő leképezésre, egyébként
pedig I(E) = hamis. |
Vegyük észre, hogy ez nem változtatja meg egy
interpretáció definícióját; ez még mindig ugyanazokból az IR, IP, IEXT, IS,
LV és IL értékekből áll. Egyszerűen csak kiterjeszti a jelentések
definiálásának szabályait egy interpretáció alatt, úgyhogy ugyanaz az
interpretáció, amelyik előállítja az igazságértékeket az alapgráfok számára,
az az üres csomópontokat tartalmazó gráfok számára is előállítja ezeket, még
akkor is, ha maguknak az üres csomópontoknak semmilyen jelentést sem ad.
Vegyük észre azt is, hogy az üres csomópontok, maguk, tökéletesen jól
definiált entitások; ezek csak abban különböznek a többi csomóponttól, hogy
nem rendeltünk hozzájuk jelentést egy interpretációval, ami azt az intuíciót
tükrözi, hogy ezeknek nincs 'globális' jelentésük (azaz nincs jelentésük azon
a gráfon kívül, amelyben definiálták őket).
Például a következő tripletekkel definiált gráf hamis az 1. ábrán
bemutatott interpretációban:
_:xxx <ex:a> <ex:b> .
<ex:c> <ex:b> _:xxx .
ugyanis, ha A' az üres csomópontot 1-re képezi le, akkor az első triplet
hamis lesz I+A'-ben, és ha 2-re képezi le, akkor pedig a második triplet lesz
hamis.
Jegyezzük meg, hogy e tripletek mindegyike, ha egy egyedülálló gráfnak
tekintenénk, igaz lenne I-ben, a teljes gráf azonban nem; továbbá, ha két
különböző csomópont-azonosítót használnánk a két tripletben, jelezve, hogy az
RDF gráfnak nem egy, hanem két csomópontja van, akkor A' az egyik csomópontot
leképezhetné 2-re, a másikat pedig 1-re, és az eredményül kapott gráf "igaz"
lenne az I interpretáció szerint.
Ez ténylegesen úgy kezeli az összes üres csomópontot, mintha ugyanaz lenne
a jelentésük, mint az egzisztenciálisan kvantifikált változóknak abban az RDF
gráfban, amelyben előfordulnak, és amelyeknek a látóköre kiterjed az egész
gráfra. Az N-Triples szintaxis értelmében ez egy olyan konvencióval
egyenértékű, amelyik a kvantorokat a gráfnak megfelelő N-Triples dokumentumon
kívülre, vagy annak a külső határára helyezné. Ez pedig azt jelenti, hogy egy
nehezen megfogható, de fontos jelentéskülönbség van a között a két művelet
között, amikor két gráf unióját képezzük, illetve amikor az egyesítésüket állítjuk elő. Két gráf
egyszerű uniója megfelel a gráfban lévő összes triplet konjunkciójának (ÉS
kapcsolatának), fenntartva mindazon üres csomópontok identitását, amelyek
mindkét gráfban előfordulnak. Ez teljesen helyénvaló, amikor a gráfban lévő
információ egyetlen forrásból jön, vagy amikor az egyiket a másikból
származtatjuk valamilyen érvényes
következtetési folyamat révén (mint pl. amikor egy következtetési szabály
alkalmazásával egy új tripletet adunk a gráfhoz). Két gráf egyesítése úgy
kezeli az üres csomópontokat, mindkét gráfban, hogy azok egzisztenciálisan
kvantifikáltak abban a gráfban, azaz, egyik gráf egyetlen üres csomópontjának
sem szabad "átkóborolnia" a másik gráfot körülvevő kvantor látóterébe. Ez
helyénvaló, amikor a gráfok különböző forrásokból jönnek, és semmi okunk
nincs azt feltételezni, hogy az egyik gráf valamelyik üres csomópontja
ugyanarra az entitásra hivatkozik, mint a másik gráf valamelyik üres
csomópontja.
A hagyományos terminológiát követve: I kielégíti E-t, ha I(E)=igaz, és az RDF gráfok egy
S halmazának (egyszerű) következménye
egy E gráf, ha minden interpretáció, mely kielégíti S minden
elemét, egyben kielégíti E-t is. A későbbi fejezetekben ezeket a fogalmakat
adaptálni fogjuk az interpretációk más osztályaihoz is, de ebben a
fejezetben, végig, 'következmény' alatt mindig egyszerű következményt
értünk.
A következmény az a kulcs-elv, mely a modell-elméleti szemantikát
a való világ alkalmazásaihoz kapcsolja. Mint már korábban megjegyeztük, egy
tényállítással tulajdonképpen azt mondjuk, hogy a világ egy olyan
interpretáció, mely a tényállításhoz az "igaz" értéket rendeli, Ha A-nak
következménye B, akkor minden interpretáció, mely igazzá teszi A-t, igazzá
teszi B-t is, úgyhogy A-nak az állítása már tartalmazza ugyanazt a
"jelentést", mint B-nek állítása; azt mondhatnánk, hogy A jelentése mintegy
tartalmazza, magában foglalja B jelentését. Ha A és B egymás következményei,
akkor mindkettő ugyanazt a dolgot "jelenti", abban az értelemben, hogy
bármelyiküket kijelentve ugyanazt mondjuk a világról. Ennek a megfigyelésnek
az érdekessége akkor mutatkozik meg igazán, amikor A és B különböző
kifejezések, minthogy ilyenkor a következmény reláció adja meg a
megfelelő szemantikai felhatalmazást arra, hogy valamely alkalmazás az
egyiket kikövetkeztetheti vagy kigenerálhatja a másikból. A formális
szemantika a kielégítés, a következmény, és az
érvényesség fogalmain keresztül egy nagyon szigorú definícióját adja
a "jelentés" fogalmának, amely közvetlenül összekapcsolható olyan számítási
módszerekkel, amelyek megállapíthatják, hogy valamely ábrázolt tudás
valamilyen transzformációja megőrzi-e annak jelentéstartalmát.
Bármely folyamatot, mely egy E gráfot
konstruál valamilyen más S gráf(ok)ból, "(egyszerűen) érvényes"-nek
nevezünk, ha E minden esetben következménye S-nek; egyébként pedig
érvénytelennek kell neveznünk. Megjegyzendő, hogy ha egy folyamat
érvénytelen, az nem jelenti, hogy a konklúzió hamis, és az érvényesség nem
garantálja, hogy a konklúzió igaz. Az érvényesség azonban a legtöbb garancia,
amit egy kijelentés-logikai nyelv ajánlhat: igaz inputból sohasem von le
hamis konklúziót.
Ez a szekció bemutat néhány alapvető eredményt az egyszerű következményről
és az érvényes következtetésről. Az egyszerű következmény már
viszonylag egyszerű szintaktikai összehasonlításokkal is felismerhető. Az
egyszerűen érvényes következtetés két alapvető formája RDF-ben, logikai
kifejezésekkel: a következtetés (P és Q)-ból P-re, és a foo(abcd)-ből a
(létezik(?x) foo(?x))-re.
Ezek az eredmények csak az egyszerű következményre érvényesek, a
következmény kiterjesztett fogalmára azonban már nem (ez utóbbiakat a későbbi
szekciókban ismertetjük). A bizonyításokat, amelyek mindegyike egyszerű, az
A. mellékletben adjuk meg; ez a melléklet
leírja a következmény néhány más tulajdonságát is, ami szintén érdekes
lehet.
Üres gráf lemma. A tripletek üres halmaza bármely gráf
következménye lehet, de a tripletek üres halmazának következménye csak önmaga
lehet. [Bizonyítás]
Részgráf lemma. Egy
gráfnak következménye minden részgráfja. [Bizonyítás]
Példány lemma. Egy
gráf következménye bármelyik példányának. [Bizonyítás]
A viszony az egyesítés és a következmény között egyszerű, és azonnal
nyilvánvalóvá válik az alábbi definíciókból:
Egyesítési lemma.
RDF gráfok egy S halmazának egyesítése S-nek következménye, S minden tagja
pedig az egyesítés következménye. [Bizonyítás]
Ez azt jelenti, hogy gráfok egy halmaza a modell-elmélet szempontjából úgy kezelhető,
mintha egyenértékű volna azok egyesítésével, azaz egyetlen gráffal. Ezzel
valamelyest rövidíthető a terminológia: így pl. a fenti "S következménye E"
definíció így is parafrazeálható: S következménye E, ha minden interpretáció,
mely kielégíti S-t, kielégíti E-t is.
Az 1.5 szekcióban megadott példa kimutatja,
hogy általában nem az a helyzet, hogy gráfok egy halmazának egyszerű uniója a
halmaz következménye lenne.
Az egyszerű RDF következtetés fő eredménye:
Interpolációs
lemma. S következménye egy E gráf, ha, és csak akkor, ha S egyik
részgráfja E egyik példánya. [Bizonyítás]
Az interpolációs lemma szintaktikai értelemben tökéletesen jellemzi az
egyszerű RDF következményt. Ahhoz, hogy meg tudjuk állapítani, hogy egy RDF
gráfhalmaznak következménye-e egy másik, ellenőriznünk kell, hogy van-e a
következménygráfnak egy olyan példánya mely az eredeti gráfhalmaz
egyesítésének egy részhalmaza. Természetesen, ehhez nem szükséges ténylegesen
létrehozni az egyesítést. Ha az E következménytől haladunk visszafelé, hatékony
technika lehet, ha a részgráf ütköztetési folyamatban az üres csomópontokat
változókként kezeljük, lehetővé téve ily módon, hogy azok egy találatot jelző
névhez kötődjenek az S-ben lévő előzmény-gráf(ok)ban –
vagyis azokban a gráfokban, amelyekből származtatható a következmény-gráf. Az Interpolációs lemma
kimutatja, hogy ez a folyamat érvényes, és még komplett is, ha az részgráf-ütköztető algoritmus is
az. A komplett
részgráf-ellenőrző algoritmusok léte azt is mutatja, hogy az RDF következmény
eldönthető, azaz, van olyan befejeződő algoritmus, mely meg tudja
határozni bármely véges S halmaz, és bármilyen E gráf esetén, hogy E
következménye-e S-nek, vagy sem.
Egy ilyen változó-összekötő folyamat csak akkor lenne helyénvaló, ha egy
tervezett következmény konklúziójára alkalmaznánk. Ez annak felel
meg, mintha a dokumentumot célként vagy kérdésként használnánk, szemben
azzal, mintha tényként állítanánk. Ha ugyanis egy RDF dokumentumot tényként
kezelünk, akkor érvénytelen lenne új értékeket kötni bármelyik üres
csomópontjához, hiszen az eredményül kapott gráf így esetleg nem lenne
következménye a tény dokumentumnak.
Az Interpolációs lemmának van egy közvetlen következménye, egy
nem-következmény kritérium:
Anonimitási lemma.
Tegyük fel, hogy E egy sovány gráf és
E' egy valódi példánya E-nek. Ekkor E' nem következménye E-nek. [Bizonyítás]
Ismét megjegyezzük, hogy ez csak az egyszerű következményre vonatkozik, és
nem azokra a szókészlet-következmény viszonyokra, amelyeket e dokumentum
további részében definiálunk.
A következmény több alapvető tulajdonsága következik még közvetlenül a
fenti definíciókból és eredményekből, de itt csak a teljesség kedvéért
említjük meg őket:
Monotonitási lemma. Tegyük fel, hogy S
egy részgráfja S'-nek, és S következménye E. Ekkor S' következménye E. [Bizonyítás]
A véges kifejezéseknek azt a tulajdonságát, hogy mindig deriválhatók
előzmények egy véges halmazából, tömörségnek (compactness) nevezzük.
Azok a szemantika-elméletek, amelyek támogatják a következmény nem-tömör
fogalmát, nem rendelkeznek az ehhez szükséges kiszámítható következtetési
rendszerekkel.
Tömörségi
lemma. Ha S következménye E, és E egy véges gráf, akkor S valamely
véges S' részhalmazának következménye E. [Bizonyítás]
2.1
Szókészlet-interpretációk és szókészlet-következmények
Az egyszerű interpretációk és az egyszerű következmények akkor tudják
megragadni az RDF gráfok szemantikáját, amikor a gráfban szereplő nevek
konkrét jelentésével egyáltalán nem foglalkoznak. Hogy megragadhassuk egy
olyan RDF gráf teljes jelentését, amelyet egy meghatározott szókészlet
segítségével írtak le, általában szükség van további szemantikai feltételek
megadására, amelyek erősebb jelentést csatolnak az egyes URI hivatkozásokhoz
és tipizált literálokhoz a gráfban. Az olyan interpretációkat, amelyeknek
extra szemantikai feltételeket kell kielégíteniük egy bizonyos szókészletre,
általános formában szókészlet-interpretációknak nevezzük. Az ilyen
interpretációkra vonatkozó következményeket pedig általános formában
szókészlet-következményeknek hívjuk. Az interpretációknak és
következményeknek ezt az erősebb fogalmát egy névtér-prefixszel jelöljük, és
így hivatkozunk rájuk, mint rdf-interpretáció, rdf-következmény,
rdfs-következmény és így tovább. Minden esetben, amikor egy szókészlet
jelentését korlátozzuk, és hozzá egzakt feltételeket asszociálunk, akkor a
szókészletet és a feltételeket egyértelműen és részletesen meg kell
adnunk.
Az RDF szókészlet, rdfV, URI
hivatkozások halmaza az rdf: névtérben:
| Az RDF szókészlet |
rdf:type
rdf:Property rdf:XMLLiteral rdf:nil rdf:List
rdf:Statement rdf:subject rdf:predicate rdf:object rdf:first rdf:rest
rdf:Seq rdf:Bag rdf:Alt rdf:_1 rdf:_2 ... rdf:value |
Az rdf-interpretációk extra szemantikai feltételeket
szabnak meg az rdfV-re, valamint az
rdf:XMLLiteral típusú tipizált literálokra, amelyeket beépített
RDF adattípusoknak is nevezünk. (Ezt az adattípust teljesen leírja
az Az RDF alapfogalmai és absztrakt
szintaxisa dokumentum [RDF-FOGALMAK]). Bármely sss
karakterláncot, amelyik kielégíti azt a feltételt, hogy benne van az rdf:XMLLiteral
lexikális terében, jól tipizált XML-literál karakterláncnak
fogjuk nevezni. Az ennek megfelelő értéket a literál XML értékének
fogjuk nevezni. Jegyezzük meg, hogy a jól tipizált XML-literálok XML értékei
precíz 1:1 arányban megfelelnek az ilyen literálok XML-literál
karakterláncainak, de maguk nem karakterláncok. Az olyan XML-literált,
amelynek a literál karakterlánca jól tipizált, jól tipizált
XML-literálnak, minden más XML-literált pedig rosszul
tipizáltnak fogunk nevezni.
Egy V szókészlet
rdf-interpretációja (V unió rdfV)-nek egy egyszerű I interpretációja, mely kielégíti
azokat az extra feltételeket, amelyeket az alábbi táblázat ír le, valamint az
összes tripletet, amelyek az utána következő táblázatban vannak felsorolva.
Ezeket a tripleteket rdf axiomatikus tripleteknek nevezzük.
RDF szemantikai feltételek
x eleme IP-nek, ha, és csak
akkor, ha <x, I(rdf:Property)> benne
van IEXT(I(rdf:type))-ban
|
Ha
"xxx"^^rdf:XMLLiteral
eleme V-nek, és xxx egy jól tipizált
XML-literál karakterlánc, akkor
IL("xxx"^^rdf:XMLLiteral)
az xxx-nek az XML értéke;
IL("xxx"^^rdf:XMLLiteral) benne
van LV-ben;
IEXT(I(rdf:type)) tartalmazza
<IL("xxx"^^rdf:XMLLiteral),
I(rdf:XMLLiteral)>-t
|
Ha
"xxx"^^rdf:XMLLiteral
eleme V-nek, és xxx egy rosszul tipizált
XML-literál karakterlánc, akkor
IL("xxx"^^rdf:XMLLiteral)
nincs benne LV-ben;
IEXT(I(rdf:type)) nem tartalmazza
<IL("xxx"^^rdf:XMLLiteral),
I(rdf:XMLLiteral)>-t.
|
Az első feltételt úgy
tekinthetjük, mint amelyik az interpretáció univerzumában lévő erőforrások
halmazaként definiálja IP-t, amelynek az értéke az I(rdf:type)
tulajdonság I(rdf:Property) értéke. Az univerzumnak az ilyen
részhalmazai központi szerepet játszanak az RDFS interpretációkban.
Megjegyzendő, hogy ez a feltétel elvárja, hogy IP részhalmaza legyen IR-nek.
A harmadik feltétel azt köti ki,
hogy a rosszul tipizált XML-literálok valami mást jelentsenek, mint
literál-értéket: ez lesz a szabványos módja a rosszul formált literálok
kezelésének.
RDF axiomatikus tripletek
rdf:type rdf:type rdf:Property
.
rdf:subject rdf:type rdf:Property .
rdf:predicate rdf:type rdf:Property .
rdf:object rdf:type rdf:Property .
rdf:first rdf:type rdf:Property .
rdf:rest rdf:type rdf:Property .
rdf:value rdf:type rdf:Property .
rdf:_1 rdf:type rdf:Property .
rdf:_2 rdf:type rdf:Property .
...
rdf:nil rdf:type rdf:List . |
A később következő 4. fejezetben leírt rdfs-interpretációk további
szemantikai feltételeket (értéktartomány- és érvényességikör-feltételeket)
rendelnek az RDF szókészletben szereplő tulajdonságokhoz, és más szemantikai
kiterjesztések még további feltételeket is kiköthetnek (MAY impose) azért,
hogy még tovább korlátozzák ezek jelentését. Követelmény azonban, hogy az
ilyen feltételeknek kompatibiliseknek kell lenniük (MUST be compatible) azokkal a
feltételekkel, amelyeket ebben a szekcióban leírunk.
Például a következő rdf-interpretáció kiterjeszti az 1. ábrán bemutatott
egyszerű interpretációt arra az esetre, ahol V tartalmazza rdfV-t is. Az egyszerűség kedvéért ebben a példában
mellőzzük az XML-literálokat.
IR = LV unió {1, 2, T , P}
IP = {1, T}
IEXT: 1=>{<1,2>,<2,1>},
T=>{<1,P>,<T,P>}
IS: ex:a=>1, ex:b=>1,
ex:c=> 2, rdf:type=>T,
rdf:Property=>P, rdf:nil=>1,
rdf:List=>P, rdf:Statement=>P,
rdf:subject=>1, rdf:predicate=>1,
rdf:object=>1, rdf:first=>1,
rdf:rest=>1, rdf:Seq=>P,
rdf:Bag=>P, rdf:Alt=>P, rdf:_1, rdf:_2, ...
=>1
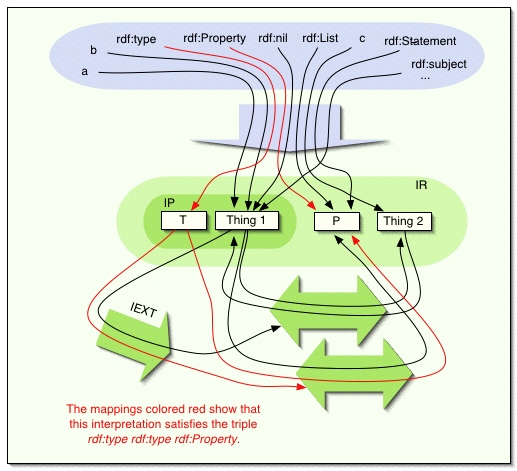
2. ábra: Egy rdf-interpretáció.
(Az ábra szövege: A piros színnel jelölt leképezések azt mutatják, hogy ez
az interpretáció kielégíti az rdf:type rdf:type rdf:property
tripletet.)
Ez nem a legkisebb rdf-interpretáció, amelyik kiterjeszthetné az előző
példát, hiszen megtehettük volna, hogy az IEXT(T) legyen
{<1,2>,<T,2>}, és kezelhettük volna anélkül, hogy P benne lenne
az univerzumban. Általában egy adott entitás egy interpretációban több
'szerepet' is játszhat egyidejűleg, addig a határig, amíg ez megtehető
anélkül, hogy megsértenénk bármelyik előírt szemantikai feltételt. A fenti
interpretáció – példaképpen – a tulajdonságokat azonosítja a
listákkal; könnyen lehet, hogy más interpretációk nem alkalmaznának ilyen
azonosítást.
Minden rdf-interpretáció
egyben egyszerű interpretáció is. A többlet-struktúra nem
akadályozza meg abban, hogy az egyszerűbb szerepet is eljátssza.
3.2. RDF-következmény
S-nek rdf-következménye E, amikor minden rdf-interpretáció, mely
kielégíti S minden elemét, egyben kielégíti E-t is. Ez a fogalmazás követi az
egyszerű következmény 2. fejezetben megadott definícióját, és csak abban tér el
attól, hogy rdf-interpretációra
hivatkozik egyszerű interpretáció helyett. Az rdf-következmény a szókészlet következmények egyik
példája.
Könnyen belátható, hogy a 2. fejezet lemmái közül
nem mindegyik alkalmazható az rdf-következményre: például az alábbi
triplet:
rdf:type rdf:type rdf:Property .
"igaz" minden rdf-interpretációban, s így az üres gráf
rdf-következménye is lehet, ami viszont ellentmond az rdf-következményre
vonatkozó interpolációs lemmának. A 7.2 szekció
leírja az rdf-következmény felismerésének egzakt feltételeit.
Az RDF szemantikai feltételei jelentős formális korlátozásokat csak a
központi RDF szókészlet jelentésére vezetnek be, így az rdf-következmény és
az rdf-interpretáció fogalmak
minden további változtatás nélkül érvényesek a szókészlet fennmaradó részére.
Ez a rész magában foglalja azt a szókészletet, amelyet konténerek és zárt
kollekciók leírására szántak, de magában foglalja az ún. tárgyiasítási
szókészletet is, mely lehetővé teszi, hogy egy RDF gráf körülírjon és
bemutasson tripleteket. Ebben a szekcióban áttekintjük ennek a szókészletnek
a szándékolt jelentéseit, és felhívjuk a figyelmet néhány olyan intuitív
következményre, amelyet nem támogat a formális modell-elmélet. A szemantikai kiterjesztések
korlátozhatják (MAY limit) ezeknek a szókészleteknek
a formális interpretációját, hogy megfeleljenek ezeknek a szándékolt
jelentéseknek.
Az intuitív következményekre vonatkozó feltételeknek a kihagyása a
formális szemantikából egy tervezési döntés volt, annak érdekében, hogy a
nyelv alkalmazkodjék az RDF használat már meglévő, különböző változataihoz,
és hogy egyszerűsödjék a formális RDF következményeket ellenőrző folyamatok
implementációja. Az alkalmazások dönthetnek pl. úgy, hogy speciális eljárási
technikákat használnak az RDF kollekciós szókészletének a megvalósítására.
| Az RDF tárgyiasító
szókészlete |
rdf:Statement rdf:subject rdf:predicate
rdf:object |
A szemantikai kiterjesztések korlátozhatják (MAY limit) ezek interpretációját,
úgyhogy egy ilyen formájú triplet:
aaa rdf:type rdf:Statement .
csak akkor lesz "igaz" I-ben, ha I(aaa) egy RDF triplet szimbóluma valamely RDF dokumentumban, és a három
tulajdonság, amikor egy így megjelölt tripletre alkalmazzuk, ugyanazokkal az
értékekkel rendelkezik, mint ennek a tripletnek a megfelelő komponensei.
Ezt illusztrálható a következő két RDF gráffal, amelyek közül az első csak
egyetlen tripletből áll:
<ex:a> <ex:b> <ex:c> .
és
_:xxx rdf:type rdf:Statement .
_:xxx rdf:subject <ex:a> .
_:xxx rdf:predicate <ex:b> .
_:xxx rdf:object <ex:c> .
A második gráfot az első gráf tárgyiasításának hívjuk; azt az üres csomópontot
pedig, amellyel a második gráfban az első gráf tripletjére hivatkozunk,
némileg zavarkeltően tárgyiasított tripletnek nevezzük. (Ez nemcsak
üres csomópont, hanem URI hivatkozás is lehet.) A tárgyiasítási szókészlet
szándékolt interpretációjában a második gráfot azzal tehetnénk igazzá egy I
interpretációban, ha úgy interpretálnánk a tárgyiasított tripletet, mintha az
az első gráf tripletjének szimbólumára hivatkozna valamilyen konkrét RDF
dokumentumban (feltéve, hogy ez a szimbólum érvényes RDF), és azután I
segítségével úgy interpretálnánk azt a szintaktikus tripletet, amelyet a
szimbólum előállít, hogy e triplet alanyának, állítmányának és tárgyának
interpretációja azonos legyen a tárgyiasításban és abban a tripletben,
amelyet a tárgyiasítás leír. Ezt (az alanyra) formálisabban így írhatnánk le:
<x,y> benne van IEXT(I(rdf:subject))-ben, ahol x egy ilyen
formátumú RDF triplet szimbóluma:
aaa bbb ccc .
és y azonos I(aaa)-val – és ugyanígy tovább, az állítmány és a
tárgy esetében is. Vegyük észre, hogy az rdf:subject tulajdonság
értéke nem az alany URI hivatkozása, maga, hanem annak az interpretációja, és
így ez a feltétel egy kétfokozatú interpretációs folyamatot feltételez: az
egyikben interpretálnunk kell a tárgyiasított csomópontot (a tárgyiasításban
lévő tripletek alanyát), hogy egy másik tripletre hivatkozzék, és azután úgy
kezelve a tripletet mint RDF szintaxist, ismét alkalmazzuk az interpretációs
leképezést, hogy megkapjuk azt, amire az alanya hivatkozik. Ez
megköveteli, hogy a tripletszimbólumok elsőrendű entitásként szerepeljenek
egy interpretáció IR univerzumában. Összefoglalva: egy tárgyiasítás jelentése
az, hogy létezik egy dokumentum, mely tartalmaz egy tripletszimbólumot, mely
ugyanazt jelenti, mint amit az első gráf jelent, bármi legyen is az.
Megjegyezzük, hogy a tárgyiasítási szókészlet ilyen felfogása nem úgy
értelmezi a tárgyiasítást, mint az idézet egy formáját, hanem úgy, hogy a
tárgyiasítás leírja azt a viszonyt, mely egy triplet szimbóluma, és azok
között az erőforrások között áll fenn, amelyekre a triplet hivatkozik.
Intuitíve a tárgyiasítást így olvassuk: "ez az RDF szakasz ezekről a
dolgokról szól", és nem úgy, hogy "ennek az RDF szakasznak ez a formája".
Az itt leírt szemantikai kiterjesztés elvárja hogy az a triplet, amelyet a
tárgyiasítás leír – a fenti példában az I(_:xxx)
–, egy konkrét szimbólum vagy triplet példány legyen egy
(valódi vagy képzeletbeli) RDF dokumentumban, és nem egy 'absztrakt' triplet,
amelyet egy nyelvtani formának tekintünk. Előfordulhat ugyanis több olyan
entitás is, mely azonos alany-állítmány-tárgy tulajdonságokkal rendelkezik.
Noha egy gráfot tripletek halmazaként definiálunk, több ilyen, azonos
struktúrájú szimbólum is előfordulhat a különböző dokumentumokban. Így akár
azt is lehetne állítani, hogy a fenti második gráfban lévő üres csomópont nem
is az első gráfban lévő tripletre hivatkozik, hanem valami más tripletre,
amelynek azonos a struktúrája. A tárgyiasításnak ezt a konkrét
interpretációját olyan alkalmazási esetek alapján választották meg, ahol
efféle tulajdonságokat alkalmaznak a tárgyiasított tripletre, mint a készítés
dátuma vagy eredet-információja, amelyeknek csak akkor van értelmük, ha
feltételezzük, hogy a szimbólum vagy a triplet egy meghatározott példányára
vonatkoznak.
Noha az RDF alkalmazások az RDF dokumentumokban tárgyiasítást
használhatnak a tripletszimbólumokra való hivatkozásra, a kapcsolatot a
dokumentum és a tárgyiasítása között az RDF gráfszintaxisán kívül eső
eszközökkel kell fenntartaniuk. (Az RDF/XML szintaxis
specifikációja [RDF-SZINTAXIS] szerint
az rdf:ID attribútumot használhatjuk egy triplet leírásában arra a célra,
hogy előállítsuk annak a tripletnek a tárgyiasítását, ahol a tárgyiasított
triplet egy URI hivatkozás lesz, amelyet a dokumentum bázis-URI-jéből,
valamint az rdf:ID értékéből mint erőforrásrész-azonosítóból
konstruálunk.) Minthogy egy triplet tárgyiasításának a
kijelentése implicite nem jelenti ki magát a tripletet, ez azt jelenti, hogy
nem áll fenn következmény-viszony a triplet és a tárgyiasítása
között. Ezért a tárgyiasítási szókészletben nincsenek is erre vonatkozó
tényleges szemantikai korlátozások azokon túl, amelyek az rdf-interpretációra is vonatkoznak.
Egy triplet tárgyiasításának tehát nem következménye a triplet, és a
tripletnek sem következménye a tárgyiasítása. (A tárgyiasítás csupán annyit
mond, hogy a tripletszimbólum létezik, és hogy miről szól, de azt nem mondja,
hogy a triplet "igaz". Ez a második nem-következmény annak a ténynek a
velejárója, hogy egy triplet kijelentése nem állítja automatikusan, hogy
létezik olyan tripletszimbólum az univerzumban, amelyet a triplet leír.
Például a triplet szerepelhet egy állatokat leíró ontológiában, amelyet egy
olyan interpretáció elégítene ki, amelyben az univerzum csak állatokat
tartalmaz; egy ilyen interpretációban ennek a tripletnek a tárgyiasítása
nyílván hamis lenne.)
Mivel az RDF gráfban/gráfokban a viszony a tripletek és azok tárgyiasítása
között nem kell, hogy egy-az-egyhez típusú legyen, egy tárgyiasítással leírt
entitás tulajdonságát megadó állításból nem szükségszerűen következik, hogy
ez a tulajdonság érvényes lesz egy másik ugyanilyen entitás esetére is. (Még
akkor sem lesz feltétlenül érvényes, ha ez a másik entitás ugyanazokból a
komponensekből áll.) Például ebből a két tárgyiasításból, és ebből az egy
tulajdonság-kijelentésből:
_:xxx rdf:type rdf:Statement .
_:xxx rdf:subject <ex:subject> .
_:xxx rdf:predicate <ex:predicate> .
_:xxx rdf:object <ex:object> .
_:yyy rdf:type rdf:Statement .
_:yyy rdf:subject <ex:subject> .
_:yyy rdf:predicate <ex:predicate> .
_:yyy rdf:object <ex:object> .
_:xxx <ex:property> <ex:foo> .
nem következik ez:
_:yyy <ex:property> <ex:foo> .
| Az RDF konténer szókészlet |
rdf:Seq rdf:Bag rdf:Alt rdf:_1 rdf:_2
... |
Az RDF szókészleteket bocsát rendelkezésünkre a konténerek három
osztályának leírásához. A konténereknek van egy típusuk, és a tagjaik
felsorolhatók rögzített számú konténertagság-tulajdonság
segítségével. Ezeket a tulajdonságokat index-számokkal láthatjuk el, hogy meg
tudjuk különböztetni őket egymástól, de ezek az indexek nem szükségszerűen
jelentenek sorrendet vagy egyéb rendezettséget magában a konténerben (néhány
konténertípust eleve rendezetlennek tekintünk).
Az alább leírt RDFS szókészlet hozzáad az RDF szókészletéhez egy generikus
tagságtulajdonságot, mely a pozíciójától függetlenül érvényes, és hozzáad
olyan osztályokat, amelyek tartalmazzák az összes konténert és
tagságtulajdonságot.
Úgy kell felfogni ezt az RDF szókészletet, mint amelyik leírja a
konténereket, és nem úgy, mint amelyik konstruálja őket, ahogy a
programnyelveknél szokásos. Ilyen nézetből a tényleges konténerek a
szemantikai univerzum entitásai, és azok az RDF gráfok, amelyek ezt a
szókészletet használják, csak nagyon alapvető információkat nyújthatnak
ezekről az entitásokról (pl. jellemezhetik a konténer típusát, és részleges
információt szolgáltathatnak a konténer tagjairól). Az RDF konténer
szókészlet ilyen korlátai miatt sok olyan 'természetes' feltételezés marad,
amelyre vonatkozóan az RDF modell-elmélete formálisan nem intézkedik. Ezt
azonban nem szabad egy olyan jelentésként értelmezni, hogy ezek a
feltételezések hamisak, hanem csupán olyannak, hogy az RDF formálisan nem
definiál olyan következményt, hogy ezeknek igazaknak kell lenniük.
Nincsenek megadva speciális szemantikai feltételek a konténer
szókészletre: az egyetlen 'struktúra', amelyet az RDF a konténerei számára
feltételez, kikövetkeztethető ennek a szókészletnek a használatából, valamint
az RDF általános szemantikai feltételeiből. Ez mindössze annyi, hogy tudja,
milyen típusú a konténer, és ismeri a konténer tagjainak a részleges
felsorolását. A szándékolt használati mód az, hogy az rdf:Bag
típusú dolgokat rendezetlennek tekintjük, és megengedjük a tagjaik
duplikációját; az rdf:Seq típusú dolgokat rendezettnek
feltételezzük, míg az rdf:Alt konténertípust alternatívák
gyűjteményének fogjuk fel, egy esetleges preferencia-sorrenddel. A rendezett
konténerekben a tagok sorrendjét a konténertagság-tulajdonságok numerikus
értéke jelzi, amelyet egyetlen értékűnek tekintünk. Ezek az informális
interpretációk azonban nem tükröződnek semmilyen formális RDF
következményben.
Az RDF nem támogat semmi olyan következményt, ami egy rdf:Bag
tagjainak különböző sorrendben történő felsorolásából származhatna. Például
ennek a felsorolásnak:
_:xxx rdf:type rdf:Bag .
_:xxx rdf:_1 <ex:a> .
_:xxx rdf:_2 <ex:b> .
nem következménye ez:
_:xxx rdf:_1 <ex:b> .
_:xxx rdf:_2 <ex:a> .
Vegyük észre, hogy ha ez a konklúzió érvényes lenne, akkor az eredeti gráffal való
egyesítésének az eredménye szintén egy érvényes következmény lenne, mely azt mondaná ki, hogy
mindkét tag előfordult mindkét pozíción. Ez annak a ténynek a következménye,
hogy az RDF egy tisztán deklaratív nyelv.
Nincs olyan feltételezés, hogy egy konténer tulajdonsága érvényes
bármelyik tagjára, vagy megfordítva.
Nincs olyan formális igény, hogy a három konténerosztály diszjunkt legyen,
úgyhogy kijelenthető például valamiről hogy az egyidejűleg
rdf:Bag és rdf:Seq is. Olyan feltételezés sincs,
hogy a konténerek tagjainak index-számozása folyamatos, úgyhogy pl. ebből a
szekvencia-konténerből:
_:xxx rdf:type rdf:Seq.
_:xxx rdf:_1 <ex:a> .
_:xxx rdf:_3 <ex:c> .
nem következik ez a triplet:
_:xxx rdf:_2 _:yyy .
Az RDF-ben nincs mód arra, hogy 'lezárjunk' egy konténert, azaz
kijelentsük, hogy rögzített számú tagja van. Ez annak a ténynek a
tükröződése, hogy – teljesen konzisztens módon – bármikor
adhatunk egy olyan tripletet egy gráfhoz, mely egy újabb tagságtulajdonságot
deklarál egy konténer számára. És végül: nincs olyan beépített feltételezés,
hogy egy RDF konténernek csak véges sok tagja lehet.
3.3.3 RDF kollekciók
| Az RDF kollekciós
szókészlete |
rdf:List rdf:first rdf:rest
rdf:nil |
Az RDF tartalmaz egy szókészletet kollekciók (azaz 'lista-struktúrák')
leírására, "fej-farok" láncok segítségével. A kollekciók különböznek a
konténerektől annyiban, hogy elágazási struktúrákat tesznek lehetővé, és
explicit záró elemmel rendelkeznek, amellyel lehetővé teszik az
alkalmazásoknak, hogy meghatározzák a kollekció elemeinek egzakt halmazát.
Ugyanúgy, mint a konténerek esetében, a kollekciós szókészletre sincsenek
megadva speciális feltételek azon kívül, hogy az rdf:nil típus
egy rdf:List. Ezt a szókészletet tipikusan olyan környezetekben
való használatra szánták, ahol a konténert üres csomópontokkal írjuk le, hogy
így összekapcsolhassuk az elemek egy 'jól formált' sorozatát, ahol az elemek
mindegyikét két ilyen formájú triplet írja le:
_:c1 rdf:first aaa .
_:c1 rdf:rest _:c2
ahol az utolsó elemet az rdf:nil használatával jelezzük,
amelyet az rdf:rest értékeként adunk meg. Egy ismerős
konvencióval az rdf:nil-t egy üres kollekciónak tekinthetjük.
Minden ilyen gráf annak kijelentésével egyenlő, hogy a kollekció létezik, és
minthogy a kollekció elemei meghatározhatók a végignézésükkel, ez gyakran
elegendő arra, hogy az alkalmazások meghatározhassák az ilyen gráf
jelentését. Megjegyzendő azonban, hogy a szemantika nem várja el, hogy
bármilyen kollekció létezzék azokon kívül, amelyek explicit módon meg vannak
említve egy gráfban (valamint az üres kollekción kívül). Például, az alábbi
kollekció létezése, amelyik két elemet tartalmaz, nem garantálja
automatikusan, hogy egy hasonló kollekció, permutált elemekkel, úgyszintén
létezik:
_:c1 rdf:first <ex:aaa> .
_:c1 rdf:rest _:c2 .
_:c2 rdf:first <ex:bbb> .
_:c2 rdf:rest rdf:nil .
ennek nem következménye ez:
_:c3 rdf:first <ex:bbb> .
_:c3 rdf:rest _:c4 .
_:c4 rdf:first <ex:aaa> .
_:c4 rdf:rest rdf:nil .
Hasonlóképpen, az RDF semmiféle 'jól formáltsági' feltételt nem köt ki ennek a
szókészletnek a használatánál, úgyhogy írhatunk olyan RDF gráfokat is,
amelyek ilyen különleges objektumok létezését is kijelenthetik, mint pl.
elágazó végű listák, nem lista-elemmel végződő listák, vagy akár többfejű
listák:
_:666 rdf:first <ex:aaa> .
_:666 rdf:first <ex:bbb> .
_:666 rdf:rest <ex:ccc> .
_:666 rdf:rest rdf:nil .
Még az is lehetséges, hogy olyan tripletek halmazát írjuk le, amelyek
alulspecifikálják a kollekciót (pl. oly módon, hogy nem adják meg az
rdf:rest tulajdonság értékét).
Szemantikai kiterjesztések megadhatnak (MAY place) extra szintaktikai
korlátozásokat (jól formáltsági feltételeket) erre a szókészletre, hogy
kizárják az ilyen jellegű gráfokat. Kitilthatják továbbá (MAY exclude) a
kollekciós szókészlet olyan interpretációit is, amelyek megsértik azt a
konvenciót, hogy a fenti formátumú, két tripletből álló, és
rdf:nil-lel végződő 'láncolt' kollekciók alanya mindig egy
teljesen rendezett sorozatot jelent, amelynek elemeit a tételek
rdf:first értékei adják, mégpedig abban a sorrendben, amelyben
az rdf:rest tulajdonságokon keresztül végigjárjuk a kollekciót
az alanytól az rdf:nil-ig. Ez a konvenció megenged olyan
sorozatokat is, amelyek más sorozatokat tartalmaznak.
Megjegyezzük, hogy az alábbiakban leírt RDFS szemantikai feltételek
megkövetelik, hogy az rdf:first tulajdonság minden alanyának, és
az rdf:rest tulajdonság minden alanyának a típusa
(rdf:type) rdf:List kell hogy legyen.
3.3.4 rdf:value
Az rdf:value szándékolt használatának intuitív magyarázata
megtalálható "Az RDF bevezető tankönyve" [RDF-BEVEZETÉS] dokumentumban. Ezt tipikusan
egy olyan tulajdonság 'elsődleges' vagy 'fő' értékének azonosítására
használjuk, amelynek több értéke lehet, vagy amelyiknek az értéke egy
összetett entitás, több saját tulajdonsággal vagy adattípus-módosító elemmel
(facet).
Mivel az rdf:value lehetséges alkalmazásainak a területe
ilyen széles, nehéz megfogalmazni erre egy olyan leírást, mely lefedné az
összes szándékolt jelentést, vagy alkalmazási esetet. A felhasználónak ezért
ügyelnie kell arra, hogy az rdf:value jelentése alkalmazásról
alkalmazásra változhat. A gyakorlatban a szándékolt jelentése gyakran
világosan kiderül a kontextusból, de könnyen elveszhet, amikor gráfokat
egyesítünk, vagy amikor konklúziókat vonunk le belőlük.
Az RDF Séma [RDF-SZÓKÉSZLET] kiterjeszti az RDF-et
egy nagyobb szókészlettel (rdfsV), amely
komplexebb szemantikai korlátozásokkal rendelkezik:
| Az RDFS szókészlet |
rdfs:domain rdfs:range rdfs:Resource
rdfs:Literal rdfs:Datatype rdfs:Class rdfs:subClassOf
rdfs:subPropertyOf rdfs:member rdfs:Container
rdfs:ContainerMembershipProperty rdfs:comment rdfs:seeAlso
rdfs:isDefinedBy rdfs:label |
(Az rdfs:comment, rdfs:seeAlso,
rdfs:isDefinedBy és az rdfs:label kifejezéseket
azért vettük fel ide, mert néhány korlátozás, mely érvényes a használatukra,
megadható az rdfs:domain, az rdfs:range és az
rdfs:subPropertyOf használatával. Ezen kívül, a formális
szemantika nem rendel hozzájuk semmi más speciális jelentést.)
Noha nem feltétlenül szükséges, de helyénvaló az RDFS szemantikáját egy új
szemantikai konstrukció, az 'osztály' fogalomkörében kifejezve megadni (az
osztály egy erőforrás, mely az univerzumban lévő, olyan dolgok halmazát
ábrázolja, amelyek mindegyikének rdf:type tulajdonsága ez az
osztály). Az osztályokat olyan dolgokként definiáljuk, amelyeknek a típusa
rdfs:Class. Egy interpretációban szereplő összes osztály
halmazát a továbbiakban IC-vel jelöljük. A szemantikai feltételeket egy, az
IC-ről IR részhalmazainak halmazára történő ICEXT leképezés értelmében adjuk
meg, ahol az ICEXT rövidítést így olvassuk: "interpretációbeli
osztálykiterjedése" (Class Extension in I).
Az ICEXT és az IC jelentését az RDFS szókészlet rdf-interpretációjában teljes mértékben definiálja
az "RDFS szemantikai feltételei" táblázat első két feltétele (lásd alább).
Figyeljük meg, hogy egy osztály kiterjedése lehet üres; továbbá, hogy (amint
azt korábban már megjegyeztük) két
különböző osztály típusú entitásnak az osztálykiterjedése lehet azonos;
valamint, hogy az rdfs:Class osztálykiterjedése tartalmazza az
rdfs:Class osztályt (azaz önmagát) is.
V-nek egy
rdfs-interpretációja egy I rdf-interpretáció (V unió rdfV unió rdfsV)-re, mely kielégíti a következő táblázatban
felsorolt szemantikai feltételeket, valamint az utána következő táblázatban
szereplő összes tripletet, amelyeket RDFS axiomatikus tripleteknek
nevezünk.
Az RDFS szemantikai feltételei
x eleme ICEXT(y)-nak ha, és csak
akkor, ha <x,y> eleme
IEXT(I(rdf:type))-nak
IC = ICEXT(I(rdfs:Class))
IR = ICEXT(I(rdfs:Resource))
LV = ICEXT(I(rdfs:Literal))
|
Ha <x,y> benne van
IEXT(I(rdfs:domain))-ben és <u,v>
benne van IEXT(x)-ben, akkor u
eleme ICEXT(y)-nak
|
Ha <x,y> benne van
IEXT(I(rdfs:range))-ben és <u,v>
benne van IEXT(x)-ben, akkor v
eleme ICEXT(y)-nak
|
Az
IEXT(I(rdfs:subPropertyOf)) reláció
tranzitív és reflexív IP-re
|
Ha <x,y> szerepel
IEXT(I(rdfs:subPropertyOf))-ban, akkor x
és y elemei IP-nek, és IEXT(x)
egy részhalmaza IEXT(y)-nak
|
Ha x eleme IC-nek,
akkor <x, I(rdfs:Resource)> szerepel
IEXT(I(rdfs:subClassOf))-ban
|
Ha <x,y> eleme
IEXT(I(rdfs:subClassOf))-nak, akkor x
és y elemei IC-nek, és ICEXT(x) egy
részhalmaza ICEXT(y)-nak
|
Az
IEXT(I(rdfs:subClassOf)) reláció tranzitív és
reflexív IC-re
|
Ha x eleme
ICEXT(I(rdfs:ContainerMembershipProperty))-nek,
akkor
< x, I(rdfs:member)> szerepel
IEXT(I(rdfs:subPropertyOf))-ban
|
Ha x eleme
ICEXT(I(rdfs:Datatype))-nak, akkor <x,
I(rdfs:Literal)> benne van
IEXT(I(rdfs:subClassOf))-ban
|
Az RDFS axiomatikus tripletjei
rdf:type rdfs:domain rdfs:Resource .
rdfs:domain rdfs:domain rdf:Property .
rdfs:range rdfs:domain rdf:Property .
rdfs:subPropertyOf rdfs:domain rdf:Property .
rdfs:subClassOf rdfs:domain rdfs:Class
.
rdf:subject rdfs:domain rdf:Statement .
rdf:predicate rdfs:domain rdf:Statement .
rdf:object rdfs:domain rdf:Statement .
rdfs:member rdfs:domain rdfs:Resource .
rdf:first rdfs:domain rdf:List .
rdf:rest rdfs:domain rdf:List .
rdfs:seeAlso rdfs:domain rdfs:Resource .
rdfs:isDefinedBy rdfs:domain rdfs:Resource .
rdfs:comment rdfs:domain rdfs:Resource .
rdfs:label rdfs:domain rdfs:Resource .
rdf:value rdfs:domain rdfs:Resource .
rdf:type rdfs:range rdfs:Class .
rdfs:domain rdfs:range rdfs:Class .
rdfs:range rdfs:range rdfs:Class .
rdfs:subPropertyOf rdfs:range rdf:Property .
rdfs:subClassOf rdfs:range rdfs:Class
.
rdf:subject rdfs:range rdfs:Resource .
rdf:predicate rdfs:range rdfs:Resource .
rdf:object rdfs:range rdfs:Resource .
rdfs:member rdfs:range rdfs:Resource .
rdf:first rdfs:range rdfs:Resource .
rdf:rest rdfs:range rdf:List .
rdfs:seeAlso rdfs:range rdfs:Resource .
rdfs:isDefinedBy rdfs:range rdfs:Resource .
rdfs:comment rdfs:range rdfs:Literal .
rdfs:label rdfs:range rdfs:Literal .
rdf:value rdfs:range rdfs:Resource .
rdf:Alt rdfs:subClassOf rdfs:Container .
rdf:Bag rdfs:subClassOf rdfs:Container .
rdf:Seq rdfs:subClassOf rdfs:Container .
rdfs:ContainerMembershipProperty rdfs:subClassOf rdf:Property .
rdfs:isDefinedBy rdfs:subPropertyOf rdfs:seeAlso .
rdf:XMLLiteral rdf:type rdfs:Datatype .
rdf:XMLLiteral rdfs:subClassOf rdfs:Literal .
rdfs:Datatype rdfs:subClassOf rdfs:Class .
rdf:_1 rdf:type rdfs:ContainerMembershipProperty .
rdf:_1 rdfs:domain rdfs:Resource .
rdf:_1 rdfs:range rdfs:Resource .
rdf:_2 rdf:type rdfs:ContainerMembershipProperty .
rdf:_2 rdfs:domain rdfs:Resource .
rdf:_2 rdfs:range rdfs:Resource .
... |
Mivel I egy rdf-interpretáció, az első feltétel implikálja, hogy
IP = ICEXT(I(rdf:Property)).
Ezekben az axiómákban és feltételekben van némi redundancia: például Az
RDF axiomatikus tripletjei, egy kivételével, származtathatók az RDFS
axiomatikus tripletjeiből, valamint az ICEXT, rdfs:domain és
rdfs:range szemantikai feltételeiből. A többi tripletet,
amelyeknek igaznak kell lenniük minden rdfs-interpretációban, az alábbi táblázat
tartalmazza:
Néhány triplet, mely rdfs-érvényességű
rdfs:Resource rdf:type rdfs:Class .
rdfs:Class rdf:type rdfs:Class .
rdfs:Literal rdf:type rdfs:Class .
rdf:XMLLiteral rdf:type rdfs:Class .
rdfs:Datatype rdf:type rdfs:Class .
rdf:Seq rdf:type rdfs:Class .
rdf:Bag rdf:type rdfs:Class .
rdf:Alt rdf:type rdfs:Class .
rdfs:Container rdf:type rdfs:Class .
rdf:List rdf:type rdfs:Class .
rdfs:ContainerMembershipProperty rdf:type rdfs:Class .
rdf:Property rdf:type rdfs:Class .
rdf:Statement rdf:type rdfs:Class .
rdfs:domain rdf:type rdf:Property .
rdfs:range rdf:type rdf:Property .
rdfs:subPropertyOf rdf:type rdf:Property .
rdfs:subClassOf rdf:type rdf:Property .
rdfs:member rdf:type rdf:Property .
rdfs:seeAlso rdf:type rdf:Property .
rdfs:isDefinedBy rdf:type rdf:Property .
rdfs:comment rdf:type rdf:Property .
rdfs:label rdf:type rdf:Property .
|
Jegyezzük meg, hogy az adattípusoknak is lehet osztálykiterjedésük, ugyanis,
ezeket szintén osztályoknak tekintjük az RDFS-ben. Amint az
rdf:XMLLiteral osztálykiterjedésére megadott szemantikai
feltételek illusztrálták, egy adattípus-osztály egyedei az adattípus értékei. Ezt a következő, 5. fejezet tárgyalja részletesebben. Az
rdfs:Literal osztály tartalmazza az összes literál értékét;
követelmény azonban, hogy azok a tipizált literálok, amelyeknek a
karakterlánca nem felel meg az adattípusuk lexikális követelményeinek, ne ebben az
osztályban rendelkezzenek jelentéssel. Az rdf-interpretációkra megadott szemantikai feltételek
implikálják, hogy az ICEXT(I(rdf:XMLLiteral)) a jól tipizált
XML-literálok minden XML értékét tartalmazzák.
Ha egyesítjük az rdf:XMLLiteral-ra és az
rdfs:range-re vonatkozó feltételeket, akkor ellentmondó
kijelentéseket is írhatunk az RDFS-ben. Ez történik, ha kijelentjük, hogy egy
tulajdonságértéknek az rdf:XMLLiteral osztályban kell lennie, de
ezt a tulajdonságot egy olyan értékkel használjuk, ami egy rosszul formált
XML-literál, és ezért nem szerepelhetne ebben az osztályban. Például:
<ex:a> <ex:p> "<nemLegálisXML"^^rdf:XMLLiteral .
<ex:p> rdfs:range rdf:XMLLiteral .
nem lehet "igaz" egyetlen rdfs-interpretációban sem, mivel
rdfs-inkonzisztens.
4.2
Extenzionális szemantikai feltételek (Informatív)
A fentebb megadott szemantikát szándékosan úgy választották meg, hogy az
RDFS szókészlet leggyengébb elfogadható interpretációja legyen. Szemantikai
kiterjesztésekkel erősíteni lehet (MAY strengthen) az értéktartomány,
az érvényességi kör, az alosztály és altulajdonság (range, domain, subclass
és subproperty) szemantikai feltételeit, a következő 'extenzionális' változatokkal:
Extenzionális alternatívák néhány RDFS szemantikai feltételre
<x,y> benne van
IEXT(I(rdfs:subClassOf))-ban, ha és csak akkor,
ha x és y elemei IC-nek és ICEXT(x)
egy részhalmaza ICEXT(y)-nak
|
<x,y> benne van
IEXT(I(rdfs:subPropertyOf))-ban, ha és csak akkor,
ha x és y elemei IP-nek és IEXT(x) egy
részhalmaza IEXT(y)-nak
|
<x,y> benne van
IEXT(I(rdfs:range))-ben, ha és csak akkor, ha
(ha <u,v> szerepel IEXT(x)-ben;
ekkor v eleme ICEXT(y)-nak)
|
<x,y> benne van
IEXT(I(rdfs:domain))-ban, ha és csak akkor, ha
(ha <u,v> szerepel IEXT(x)-ben;
ekkor u eleme ICEXT(y)-nak)
|
amelyek garantálnák, hogy az altulajdonsága és
alosztálya tulajdonságok tranzitívak és reflexívek lennének, de
ezeknek további következményeik is lennének.
Ezek az erősebb feltételek triviálisan kielégíthetők lennének az RDFS extenzionális szemantikájával,
ha a tulajdonságokat tulajdonságkiterjedésekkel, az osztályokat
osztálykiterjedésekkel azonosítanánk, és az rdfs:SubClassOf
(alosztálya) alatt pedig a részhalmaza fogalmat érthetnénk. Néha az
extenzionális változatok egyszerűbb szemantikát eredményeznek, de komplexebb
következtetési szabályokat igényelnek. Az 'intenzionális' szemantika, amelyet
a fő szövegrészben ismertetünk, az alosztály- és altulajdonság kijelentések
leggyakrabban használt változatát kínálja, és lehetővé teszi, hogy
egyszerűbben implementáljuk az RDFS-következmény szabályainak komplett halmazát, ahogy a 7.3 szekció leírja.
Habár az rdfs-interpretációra
vonatkozó szemantikai feltételek tartalmazzák azt az intuitíve ésszerű
feltételt, hogy az ICEXT(I(rdfs:Literal))-nak LV halmaznak kell
lennie, nincs lehetőség arra, hogy kikössük ezt a feltételt egy RDF
kijelentésben vagy következtetési szabályban. Ez a korlát abból a tényből
ered, hogy az RDF nem engedi meg literálok használatát a tripletek alanyának
helyén, és ezzel szigorúan behatárolja, hogy mit lehet kimondani a
literálokról az RDF-ben. Hasonlóképpen, noha kijelenthetünk tulajdonságokat
az rdfs:Literal osztályról, ezekből semmi sem vihető át magukra
a literálokra.
Például egy ilyen formátumú triplet:
<ex:a> rdf:type rdfs:Literal .
konzisztens még akkor is, ha 'ex:a' egy URI hivatkozás, és
nem egy literál. Ez azt mondja ki, hogy I(ex:a) egy
literál-érték, vagyis, hogy az 'ex:a' URI hivatkozás egy
literál-értéket jelöl. De nem specifikálja pontosan, hogy milyen
literál-értéket jelöl.
A szemantikai feltételek garantálják, hogy bármely tripletnek, amelyik
tárgyként egy típus nélküli literált tartalmaz, következménye egy hasonló
triplet, amelynek a tárgya egy üres csomópont. Ennek a tripletnek:
<ex:a> <ex:b> "10" .
a következménye egy ilyen triplet:
<ex:a> <ex:b> _:xxx .
Ez azt jelenti, hogy a literál egy entitást jelöl meg, amelynek ily módon
nevet is adhatnánk (legalábbis elvben) egy URI hivatkozás formájában.
4.4
RDFS-következmény
S rdfs-következménye E, ha minden rdfs-interpretáció, mely kielégíti S minden elemét,
egyszersmind kielégíti E-t is. Ez a fogalmazás követi az egyszerű következmény 2.
fejezetben megadott definícióját, és csak abban tér el attól, hogy rdfs-interpretációra hivatkozik
egyszerű interpretáció helyett. Az rdfs-következmény a szókészlet-következmények egy újabb példája.
Mivel minden rdfs-interpretáció egyben rdf-interpretáció is, ezért, ha S rdfs-következménye
E, akkor S rdf-következménye is E; az rdfs következmény azonban erősebb, mint
az rdf-következmény. Még az üres gráfnak is van egy nagyszámú
rdfs-következménye, amelyek nem rdf-következmények. Például minden ilyen
formátumú triplet:
xxx rdf:type rdfs:Resource .
"igaz" bármilyen szókészlet minden rdfs-interpretációjában, amelyik tartalmazza a xxx
URI hivatkozást.
Egy rdfs-inkonzisztens gráf rdfs-következménye bármilyen gráf (a
következmény definíciója alapján); az inkonzisztens halmazok ilyen 'triviális
következményeit' azonban a gyakorlatban nem nagyon érdemes konklúzióként
levonni.
Az RDF lehetővé teszi RDF-en kívül definiált adattípusok használatát, és ezeket egy-egy konkrét
URI hivatkozással azonosítja. Rendelkezik azonban egyetlen beépített
adattípussal, és ez az rdf:XMLLiteral. A nagyobb általánosság
érdekében az RDF kevés követelményt támaszt az adattípusokkal szemben.
Az adattípusok RDF szemantikája tehát minimális. Nem gondoskodik pl.
arról, hogy összekapcsoljon egy adattípust egy tulajdonsággal oly módon, hogy
ez érvényes legyen a tulajdonság minden értékére, és arra sem nyújt semmilyen
módot, hogy explicite kijelentsük, hogy egy üres csomópont egy meghatározott
adattípust jelöl. Az RDF szemantikai kiterjesztése és későbbi verziói jobban
kidolgozott adattipizálási feltételeket is bevezethetnek majd. A szemantikai
kiterjesztések hivatkozhatnak más típusú információkra is egy adattípussal
kapcsolatban (például az értékterek különböző elrendezéseire).
Az adattípus egy
olyan entitás, amelyet egyfelől karakterláncok halmaza jellemez, amelyeket
lexikális formáknak nevezünk, másfelől pedig egy olyan leképezési
szabály, mely ezt a halmazt értékek halmazának felelteti meg. Az, hogy ezek a
halmazok és leképezési szabályok miképpen vannak definiálva, az már az RDF-en
kívül eső téma.
Formálisan, egy d adattípust három dolog definiál:
1. karakterláncoknak egy nem üres halmaza, amelyet d lexikális
terének nevezünk;
2. egy nem üres halmaz, amelyet d értékterének hívunk;
3. egy leképezés d lexikális teréről, d értékterére, amelyet d
lexikális-érték leképezésének szoktunk nevezni (lexical-to-value
mapping, vagy L2V).
Ennek megfelelően, a d adattípus lexikális-érték leképezését L2V(d).
formában írjuk.
A szemantika meghatározásánál feltételezzük, hogy az interpretációk az
adattípusok meghatározott halmazához vannak viszonyítva, amelyek mindegyikét
egy URI hivatkozás azonosítja.
Formálisan: legyen D
olyan párok halmaza, amelyek egy URI hivatkozásból és egy adattípusból állnak, és ahol egyetlen URI hivatkozás
sem jelenik meg kétszer a halmazban, úgyhogy D egy leképező függvénynek
tekinthető URI hivatkozások halmazáról adattípusok halmazára; hívjuk ezt
adattípus-leképezésnek. (Az egyes URI hivatkozásokat explicit módon
ki kell írni, hogy biztosíthassuk: az interpretációk megfelelnek bármilyen
névkonvenciónak, amelyet az adattípusok definiálásáért felelős külső
szervezetek elvárnak.) Minden adattípus-leképezésről feltételezzük, hogy az
tartalmazza az <rdf:XMLLiteral, x> szabályt, ahol x az a
beépített XML-literál adattípus, amelynek lexikális tere és értéktere,
valamint lexikális-érték leképezése Az RDF alapfogalmai és absztrakt
szintaxisa [RDF-FOGALMAK]
dokumentumban van definiálva.
Továbbá, azt az adattípus-leképezést, mely tartalmazza az összes
olyan párok halmazát, amelyek formája
<http://www.w3.org/2001/XMLSchema#sss,
sss>, ahol sss egy beépített adattípus, amely
sss néven szerepel az XML Schema Part 2: Datatypes
[XML-SCHEMA2] dokumentumban, és
amelyeket az alábbi táblázat is felsorol, XSD-nek nevezzük ebben a
dokumentumban.
| XSD adattípusok |
xsd:string,
xsd:boolean,
xsd:decimal,
xsd:float,
xsd:double,
xsd:dateTime,
xsd:time,
xsd:date,
xsd:gYearMonth,
xsd:gYear,
xsd:gMonthDay,
xsd:gDay,
xsd:gMonth,
xsd:hexBinary,
xsd:base64Binary,
xsd:anyURI,
xsd:normalizedString,
xsd:token,
xsd:language,
xsd:NMTOKEN,
xsd:Name,
xsd:NCName,
xsd:integer,
xsd:nonPositiveInteger,
xsd:negativeInteger,
xsd:long,
xsd:int,
xsd:short,
xsd:byte,
xsd:nonNegativeInteger,
xsd:unsignedLong,
xsd:unsignedInt,
xsd:unsignedShort,
xsd:unsignedByte,
xsd:positiveInteger |
A többi beépített XML Séma adattípus különféle okokból alkalmatlan, és
ezért nem célszerű használni őket (SHOULD NOT be used). Így pl.
az xsd:duration
nem rendelkezik jól definiált értéktérrel (lehet, hogy az XML Séma
adattípusok későbbi verziói változtatnak ezen, és akkor ez a javított
adattípus használható lesz az RDF adattipizálásában is); az xsd:QName
és az xsd:ENTITY
egy befogadó XML dokumentum-kontextust igényel; az xsd:ID
és az xsd:IDREF
XML dokumentumon belüli kereszthivatkozásokra szolgál; az xsd:NOTATION
típust nem közvetlen használatra szánták; az xsd:IDREFS,
xsd:ENTITIES
és az xsd:NMTOKENS
pedig sorozat-értékű adattípusok, amelyek nem illeszkednek bele az RDF adattípus-modelljébe.
Ha D egy adattípus-leképezés, akkor egy V szókészlet
D-interpretációja V-nek bármilyen I rdfs-interpretációja az unió {aaa: < aaa, x >
D-ben némely x-re }, mely kielégíti az alábbi extra feltételeket a D-ben
szereplő minden < aaa, x > pár esetén.
Általános szemantikai feltételek az adattípusokra
| Ha <aaa,x> benne van D-ben,
akkor I(aaa) = x |
| Ha <aaa,x> benne van D-ben,
akkor ICEXT(x) az x értéktere és LV
részhalmaza |
Ha <aaa,x> benne van D-ben,
akkor V-ben minden "sss"^^ddd tipizált literál
számára, ahol I(ddd) = x ,
ha sss benne van x lexikális
terében, akkor IL("sss"^^ddd) = L2V(x)(sss),
egyébként IL("sss"^^ddd) nem eleme
LV-nek |
Ha <aaa,x> benne van D-ben, akkor
I(aaa) eleme
ICEXT(I(rdfs:Datatype))-nak |
Az első feltétel biztosítja, hogy I a megadott adattípus-leképezésnek megfelelően interpretálja
az URI hivatkozást. Megjegyzendő, hogy ez nem zárja ki, hogy más URI
hivatkozások is ugyanezt az adattípust jelentsék.
A második feltétel biztosítja, hogy egy adattípus URI hivatkozása, amikor
osztálynévként használjuk, az adattípus értékterére hivatkozzék, és hogy az
értéktér minden eleme literál-érték legyen.
A harmadik feltétel garantálja, hogy a tipizált literálok a szókészletben
tiszteletben tartják az adattípus lexikális-érték leképezését. Például, ha I
egy XSD-interpretáció, akkor I("15"^^xsd:decimal)-nak a
tizenötös számértéknek kell lennie. A feltétel azt is megköveteli, hogy egy
rosszul tipizált literál, amelynél a literál karakterlánc nincs az
adattípus lexikális terében, ne
jelentsen semmilyen literál-értéket. Intuitíve, egy ilyen név ugyan nem
jelent semmilyen értéket, de hogy elkerüljük a szemantikai bonyolultságot,
ami az üres nevek miatt keletkezik, a szemantika megköveteli, hogy egy ilyen
tipizált literál inkább egy 'tetszőleges' nem-literál értéket jelentsen. Így
például, ha I egy XSD-interpretáció, akkor minden ami kikövetkeztethető az
I("arthur"^^xsd:decimal)-ról, az csak annyi, hogy nincs benne
LV-ben, vagyis, nincs benne ICEXT(I(rdfs:Literal))-ban. Egy
rosszul tipizált literál nem önmaga okoz inkonzisztenciát, hanem egy olyan
gráf, amelynek a következménye az, hogy egy rosszul tipizált literál típusa
(rdf:type) mégis rdfs:Literal, vagy hogy egy
rosszul tipizált XML-literál típusa (rdf:type) mégis
rdf:XMLLiteral lesz, ami inkonzisztens lenne.
Megjegyzendő, hogy ez a harmadik feltétel csak adattípusokra érvényes D értéktartományában. Azokat a
tipizált literálokat, amelyeknek a típusa nincs benne az interpretáció adattípus-leképezésében, ugyanúgy
kezeljük, mint az előbb, vagyis, mintha valamilyen ismeretlen dolgot
jelentenének. A feltétel nem köti ki, hogy a tipizált literálban lévő URI
hivatkozás ugyanaz legyen, mint ami az adattípushoz van asszociálva. Ez lehetővé tesz olyan
szemantikai kiterjesztéseket, amelyek azonossági feltételeket definiálhatnak
az URI hivatkozásokra, hogy ezekből megfelelő konklúziókat lehessen
levonni.
A negyedik feltétel azt biztosítja, hogy az rdfs:Datatype
osztály tartalmazza azokat az adattípusokat, amelyeket bármilyen kielégítő D-interpretációban használunk.
Figyeljük meg, hogy ez egy szükséges, de nem elégséges feltétel; ez lehetővé
teszi, hogy az I(rdfs:Datatype) osztály más adattípusokat is tartalmazzon.
Az rdf-interpretációkra vonatkozó szemantikai
feltételek elvárják az 'rdf:XMLLiteral' adattípus segítségével tipizált
literálok korrekt interpretációját. A D-interpretációk azonban entitásként
létezőnek ismerik fel az adattípust, tehát nem pusztán egy szemantikai
feltételnek, amelyet az RDF tipizált literálok szintaxisára kikötünk. Ezért
azok a szemantikai kiterjesztések, amelyek azonossági feltételeket képesek
megadni az erőforrásokra, erősebb konklúziókat tudnának levonni a D-interpretációkból, mint az rdfs-interpretációkból.
Ha a D
adattípus-leképezésben lévő adattípusok diszjunktivitási feltételeket szabnak meg
az értékterükre, előfordulhat, hogy egy RDF gráfnak nem lesz olyan D-interpretációja, amelyik
kielégítené. Például az XML Séma diszjunktként definiálja az
xsd:string és xsd:decimal értékterét, s ezért
lehetetlen egy olyan XSD-interpretációt definiálni, mely kielégítené az alábbi gráfot:
<ex:a> <ex:b> "25"^^xsd:decimal .
<ex:b> rdfs:range xsd:string .
Ezt a szituációt úgy lehetne jellemezni, hogy azt mondjuk: a gráf
XSD-inkonzisztens, vagy általánosabban, hogy ez egy adattípus
ütközés. Megjegyezzük, hogy lehetne konstruálni egy kielégítő rdfs-interpretációt ehhez a gráfhoz, de ez
megsértené az XSD feltételeket, mivel az I(xsd:decimal) és az
I(xsd:string) osztálykiterjedésének ilyenkor lenne egy nem-üres
halmazmetszete.
Adattípus ütközések egyéb módokon is előállhatnak. Például bármilyen
állítás, amelyik azt mondja, hogy valami benne van e két diszjunkt adattípus
osztály mindegyikében:
_:x rdf:type xsd:string .
_:x rdf:type xsd:decimal .
vagy hogy egy tulajdonság, amelynek az értéktartománya 'lehetetlen',
értékként ezt tartalmazza:
<ex:p> rdfs:range xsd:string .
<ex:p> rdfs:range xsd:decimal .
_:x <ex:p> _:y .
egy adattípus ütközést okozna. De egy adattípus ütközés keletkezhetne egy
különleges lexikális forma használatából is. Például:
<ex:a> <ex:p> "2.5"^^xsd:decimal .
<ex:p> rdfs:range xsd:integer .
vagy egy rosszul tipizált lexikális formából is:
<ex:a> <ex:p> "abc"^^xsd:integer .
<ex:p> rdfs:range xsd:integer .
Az adattípus ütközés az egyedüli inkonzisztencia, amelyet ez a modell-elmélet felismer;
jegyezzük meg azonban, hogy olyan adattípus ütközések, amelyekben
XML-literálok szerepelnek, keletkezhetnek az RDFS-ben.
Ha D részhalmaza D'-nek, akkor egy gráf interpretációinak
D'-interpretációra történő korlátozása egy szemantikai kiterjesztést jelent a
D-re megadott azonos korlátozáshoz képest. Ugyanis, az adattípus-leképezés tulajdonképpen implicit
állításokat tesz a tipizált literálokról azáltal, hogy megköveteli tőlük:
olyan entitásokat jelentsenek, amelyek benne vannak egy adattípus értékterében. Azok az extra szemantikai
korlátozások tehát, amelyeket egy nagyobb adattípus-leképezéshez asszociálunk, kikényszeríti
az interpretációktól, hogy több tripletet tegyenek igazzá, de ugyanakkor,
ezek a korlátozások felszínre hozhatnak adattípus ütközéseket és adattípus
sértéseket is, s így egy D-konzisztens gráf könnyen D'-inkonzisztens
lehet.
Mondjuk, hogy egy RDF gráf felismer egy aaa adattípus URI
hivatkozást, amikor a gráf következménye egy ilyen formájú adattipizáló
triplet:
aaa rdf:type rdfs:Datatype .
Az rdfs-interpretációkra
vonatkozó szemantikai feltételek megkövetelik az
'rdf:XMLLiteral' beépített adattípus URI hivatkozásának
felismerését.
Ha egy gráfban minden felismert URI hivatkozás egy ismert adattípus neve, akkor létezik egy DG
természetes adattípus-leképezés, mely összepárosítja az összes
URI hivatkozást a neki megfelelő adattípussal (valamint az
'rdf:XMLLiteral'-t az rdf:XMLLiteral-lal). Ekkor a
gráf bármely I rdfs-interpretációjának létezik egy 'természetes'
DG-interpretációja, mely ugyanolyan mint I, azzal a különbséggel I(aaa) a
megfelelő adattípus, és az
rdfs:Datatype osztálykiterjedése is ennek megfelelően módosul.
Az alkalmazások megkövetelhetik (MAY require), hogy az RDF gráfok
interpretálása olyan D-interpretációk alapján történjék, ahol D a gráf egy
természetes adattípus-leképezését tartalmazza. Ez azzal egyenértékű, hogy az
adattipizáló tripleteket úgy kezeljük, mint az adattípusok gráf általi 'deklarációját', továbbá,
hogy a negyedik szemantikai feltételt átalakítjuk 'ha és csak akkor, ha'
típusú feltétellé. Megjegyzendő azonban, hogy egy adattipizáló triplet
önmagában nem biztosítja a szükséges információt annak ellenőrzéséhez, hogy a
gráf kielégíti-e a többi adattípus szemantikai feltételt, és formálisan nem
zár ki más interpretációkat sem, úgyhogy ennek a követelménynek egy formális
következmény-alapelvként történő adoptálása megsértené az általános monotonitási lemmát, amelyet
alább, a 6. fejezetben tárgyalunk
részletesebben.
5.2 A D-következmény
S D-következménye E, ha minden D-interpretáció, mely kielégíti S minden elemét,
egyszersmind kielégíti E-t is. Ez a megfogalmazás követi az egyszerű következmény 2. fejezetben megadott definícióját, és csak abban tér el
attól, hogy D-interpretációra
hivatkozik az összes egyszerű interpretáció helyett. A D-következmény a szókészlet következmények egy
újabb példája.
Mint fentebb már megjegyeztük, előfordulhat, hogy egy gráf, mely
konzisztens az egyik szókészletben, inkonzisztenssé válik egy olyan
szemantikus kiterjesztésben, amelyet egy nagyobb szókészletre definiálunk, és
a D-interpretációk megengedik az ilyen inkonzisztenciákat egy RDF ráfban. A
szókészlet következmények
definíciója azt jelenti, hogy egy inkonzisztens gráfnak bármilyen
gráf a következménye lehet az erősebb szókészlet következményben. Például,
egy D-inkonzisztens gráf D-következménye minden RDF gráf. Ennek ellenére,
általában nem célszerű az ilyen 'triviális' következményeket hasznos
következményeknek tekinteni, mert ezek esetleg nem lesznek érvényes következmények egy kisebb szókészletben.
6. A szemantikai kiterjesztések
monotonitása
Legyen adott RDF gráfok egy halmaza; Ehhez többféle módon adhatunk újabb
információt: bármelyik gráf kaphat újabb tripleteket; a gráfok halmaza extra
gráfokkal bővülhet; vagy a gráf szókészletét interpretálhatjuk a szókészlet következmény egy
erősebb fogalmához (azaz a szemantikai feltételek egy nagyobb halmazához)
viszonyítva, amelyeket az interpretációkkal szemben támasztunk. Mindez úgy
tekinthető, mint információk hozzáadása, mely több következményt tesz
érvényessé a gráf számára, mint amennyi a hozzáadás előtt érvényes volt. Ezek
a bővítések mind monotonok, abban az értelemben, hogy
azok a következmények, amelyek fennálltak a bővítés előtt, azután is
fennállnak. Ezt egy egyszerű lemmában foglalhatjuk össze:
Általános monotonitási lemma.
Tételezzük fel, hogy S és S' RDF gráfok halmazai, ahol S minden eleme S'
valamelyik elemének a részhalmaza. Tételezzük fel, továbbá, hogy Y az X
szemantikai kiterjesztését szimbolizálja; ekkor S-nek X-következménye E, úgy
hogy S és E kielégíti Y minden szintaktikai korlátozását. Így S'
Y-következménye továbbra is E.
És különösen, ha D' egy adattípus-leképezés, továbbá D egy részhalmaza
D'-nek, akkor: ha S D-következménye E, akkor S D-következménye szintén
E.
7. A következtetés szabályai
(Informatív)
Az alábbi táblázatok felsorolnak néhány következtetési mintát, amelyekkel
megragadhatók a szókészlet-következmények bizonyos formái, és amelyeket
vezérfonalként használhatunk az RDF gráfok RDF- és RDFS-következményeit
ellenőrző szoftverek tervezésénél. Az implementációk alapulhatnak a szabályok
generatív vagy komparatív alkalmazásán. Ez utóbbi esetben úgy kezelhetik a
konklúziót, mint olyan mintát, amelyet fel kell ismerniük a tervezett
következményben oly módon, hogy visszafelé haladva keresik a megfelelést más
szabályok konklúzióival, vagy a tervezett előzménnyel. Természetesen más
stratégiák is lehetségesek.
Az összes szabályt ilyen értelemben adjuk meg: adj a gráfhoz egy
tripletet, amikor az olyan tripleteket tartalmaz, amelyek megfelelnek a
mintának, és amelyek mindegyike érvényes a következő formában: a gráf
következménye (a listának megfelelő értelemben) egy bármilyen, nagyobb gráf,
amelyhez úgy jutunk, hogy a szabályokat az eredeti gráfra alkalmazzuk. Vegyük
észre, hogy egy ilyen szabály alkalmazása a gráfra azzal egyenértékű, hogy a
gráf egy egyszerű uniót (tehát nem egy egyesítést) alkot a konklúzióval, és így átmenti a
gráfban meglévő összes üres csomópontot.
Ezeknek a szabályoknak a leírásánál ezt a konvenciót követjük: az aaa, bbb
stb. kifejezések olyan URI hivatkozások helyett állnak, amelyek egy triplet
bármilyen lehetséges állítmányát jelentik; az uuu, vvv stb. kifejezések olyan
URI hivatkozásokat vagy ürescsomópont-azonosítókat szimbolizálnak, amelyek
egy triplet bármilyen lehetséges alanyát jelentik; az xxx, yyy stb.
kifejezések olyan URI hivatkozások, ürescsomópont-azonosítók vagy literálok
helyett állnak, amelyek egy triplet tárgyát jelentik; az lll egy literált, az
_:nnn forma pedig egy ürescsomópont-azonosítót jelent.
7.1 Az egyszerű következmény
szabályai
A 2. fejezetben ismertetett interpolációs lemma az alábbi
következményképző szabályokkal jellemezhető; ezek általánosítást, vagyis
olyan gráfot generálnak, amelynek az eredeti gráf az egyik példánya (más
szóval: egyede, vagy előfordulása, angolul: instance). A részgráf jelleg nem
igényel külön erre az esetre megfogalmazott triplet következmény szabályokat.
Egyszerű következmény-szabályok
A szabály
neve |
Ha E tartalmaz
egy ilyent |
akkor add a gráfhoz ezt |
| se1 |
uuu aaa xxx . |
uuu aaa _:nnn .
(ahol _:nnn egy üres csomópont, mely hozzá van rendelve xxx-hez az se1 vagy se2
szabályban.) |
| se2 |
uuu aaa xxx . |
_:nnn aaa xxx .
(ahol _:nnn egy üres csomópont, mely hozzá van rendelve uuu-hoz az se1 vagy se2
szabályban.) |
Az a kifejezés, hogy 'hozzá
van rendelve', azt jelenti, hogy a megadott szabályoknak ugyanarra az URI
hivatkozásra, üres csomópontra vagy literálra történő korábbi alkalmazása már
elő kellett hogy állítsa az üres csomópontot, vagy ha nincs ilyen üres
csomópont, akkor annak egy 'új' csomópontnak kell lennie, amely nem szerepel
a gráfban. Ez a meglehetősen bonyolult feltétel biztosítja, hogy az
eredményül kapott gráf, amelyet az új üres csomópontok hozzáadásával kapunk,
az eredeti gráfot saját, valódi példányaként tartalmazza, valamint, hogy
minden ilyen gráfnak lesz egy olyan részgráfja, mely azonos azzal, ami
generálható ezekkel a szabályokkal. Például ez a gráf:
<ex:a> <ex:p> <ex:b> .
<ex:c> <ex:q> <ex:a> .
kiterjeszthető a következőképpen:
_:x <ex:p> <ex:b> . se1 által, egy új
_:x révén, mely ex:a-hoz van rendelve
<ex:c> <ex:q> _:x . se2 által, egy létező _:x
révén, mely ex:a-hoz van rendelve
_:x <ex:p> _:y . se2 által, egy új _:y révén, mely
ex:b-hez van
rendelve
de nem lenne korrekt az első gráfból következőket levezetni:
** _:x <ex:q> <ex:a> . ** se2 által (**
mivel _:x nincs
hozzárendelve ex:c-hez)
Ezek a szabályok lehetővé teszik az üres csomópontok elszaporodását, és
ezáltal egy nagyon 'kövér' (nem-sovány) gráf előállítását; a szabályok így érvényesítik a
következményt:
<ex:a> <ex:p> <ex:b> .
<ex:a> <ex:p> _:x . xse1 által, ahol _:x hozzá van rendelve ex:b-hez
<ex:a> <ex:p> _:y .
_:z <ex:p> _:y . xse2 által, ahol _:z hozzá van rendelve ex:a-hoz
_:u <ex:p> _:y . xse2 által, ahol _:u hozzá van rendelve _:z-hez
_:u <ex:p> _:v . xse1 által, ahol _:v hozzá van rendelve _:y-hoz
Könnyen belátható tehát, hogy S egy példánya E-nek, ha és csak akkor, ha E
levezethető S-ből ezeknek a szabályoknak egy megfelelő sorrendben történő
alkalmazásával; a szükséges szabályalkalmazások kideríthetők a példány
leképezésének vizsgálatából. Így, az Interpolációs lemma alapján: S egyszerű
következménye E, ha és csak akkor, ha (az) E-t (tartalmazó gráfot) le tudjuk
vezetni S-ből ezeknek a szabályoknak az alkalmazásával. De az is világos,
hogy a szabályok naiv módon történő alkalmazása nem eredményezne hatékony
keresési folyamatot, mivel a szabályok nem fognak befejeződni, és egyenértékű
tripletek tetszőlegesen sok redundáns levezetését produkálhatják.
A tetszőleges RDF gráfok közötti egyszerű következmény meghatározásának
általános problémája eldönthető, de kevéssé valószínű, hogy gyors lefutású
algoritmussal, mert a komplexitási elmélet szerint ez a döntési probléma ún.
'NP-kamplett' osztályú. Ez kimutatható azáltal, hogy bekódoljuk egy
tetszőleges irányított gráf egy részgráfjának következményként történő
felismerését, úgy, hogy kizárólag üres csomópontokkal ábrázoljuk a gráfot
(Jeremy Carroll-tól származó megfigyelés)
Az RDF és RDFS következmények felismerésére szolgáló következő szabályok
halmaza az se1 szabály egyik speciális esetétét használja,
mely csak literálokra érvényes:
literál általánosítási szabály
A szabály
neve |
Ha E tartalmaz
egy ilyent |
akkor add a gráfhoz ezt |
| lg |
uuu aaa lll .
|
uuu aaa _:nnn .
ahol _:nnn egy üres csomópont, hozzárendeve az lll literálhoz ezzel a
szabállyal. |
Megjegyezzük, hogy ez a szabály éppen elégséges ahhoz, hogy reprodukálja E
bármelyik részgráfját, mely olyan tripletekből áll, amelyek mindegyike
tartalmaz egy adott literált, mint izomorf részgráfot, amelyben a literált
egy egyedi üres csomóponttal helyettesítettük. Ennek a jelentősége abból
fakad, hogy egy RDF triplet alanya helyén állhat üres csomópont, s ez
lehetővé teszi, hogy konklúziókat vonjunk le a többi szabály segítségével,
amelyek az adott literál által reprezentált literál-érték tulajdonságait
fejezik ki.
Az RDFS következményhez egy további szabály szükséges, mely megfordítja a
fenti lg szabályt:
literál konkretizálási szabály
A szabály
neve |
Ha E tartalmaz egy ilyent |
akkor add a gráfhoz ezt |
| gl |
uuu aaa _:nnn .
ahol _:nnn egy üres csomópont, hozzárendeve az lll literálhoz az lg szabállyal.
|
uuu aaa lll .
|
Nyilvánvaló, hogy a gl szabály redundanciát fog
produkálni, kivéve azokat az eseteket, ahol a hozzárendelt üres csomópontot
egy új triplet tárgy pozíciójába vezettük be valamilyen más
következtetési szabály segítségével. Ezeknek a szabályoknak a hatása az, hogy
biztosítják: bármelyik triplet, amelyik egy literált tartalmaz, és az a
hasonló triplet, amelyik a hozzárendelt üres csomópontot tartalmazza, mindig
levezethetők egymásból, úgyhogy egy literál azonosítható a hozzárendelt üres
csomóponttal, abból a célból, hogy ezeket a szabályokat alkalmazhassuk.
7.2 Az RDF-következmény
szabályai
RDF-következmény szabályok
A szabály
neve |
Ha E tartalmaz egy ilyent |
akkor add a gráfhoz ezt |
| rdf1 |
uuu aaa yyy . |
aaa rdf:type rdf:Property . |
| rdf2 |
uuu aaa lll .
ahol lll egy jól tipizált XML-literal . |
_:nnn rdf:type rdf:XMLLiteral .
ahol _:nnn egy üres csomópont, hozzárendeve az lll literálhoz az lg szabály segítségével .
|
Ezek a szabályok komplettek a következő értelemben:
RDF következmény lemma. S rdf-következménye E, ha és csak akkor, ha létezik egy
olyan gráf, mely levezethető S-ből plusz az RDF axiomatikus tripletekből az lg szabály és az RDF következmény-szabályok alkalmazásával, és amelynek
egyszerű következménye E. (Bizonyítás az A.
függelékben).
Megjegyezzük, hogy ez nem igényli a gl
szabály használatát.
7.3 Az RDFS-következmény
szabályai
RDFS-következmény szabályok
A szabály
neve |
Ha E tartalmaz egy ilyent |
akkor add a gráfhoz ezt |
| rdfs1 |
uuu aaa lll.
ahol lll egy típus nélküli literál (egy nyelv-teggel, vagy a
nélkül).
|
_:nnn rdf:type rdfs:Literal .
ahol _:nnn egy üres csomópont, hozzárendeve az lll literálhoz az lg szabály segítségével.
|
| rdfs2 |
aaa rdfs:domain xxx .
uuu aaa yyy .
|
uuu rdf:type xxx . |
| rdfs3 |
aaa rdfs:range xxx .
uuu aaa vvv .
|
vvv rdf:type xxx . |
| rdfs4a |
uuu aaa xxx . |
uuu rdf:type rdfs:Resource . |
| rdfs4b |
uuu aaa vvv. |
vvv rdf:type rdfs:Resource . |
| rdfs5 |
uuu rdfs:subPropertyOf vvv .
vvv rdfs:subPropertyOf xxx .
|
uuu rdfs:subPropertyOf xxx . |
| rdfs6 |
uuu rdf:type rdf:Property . |
uuu rdfs:subPropertyOf uuu . |
| rdfs7 |
aaa rdfs:subPropertyOf bbb .
uuu aaa yyy .
|
uuu bbb yyy . |
| rdfs8 |
uuu rdf:type rdfs:Class .
|
uuu rdfs:subClassOf rdfs:Resource . |
| rdfs9 |
uuu rdfs:subClassOf xxx .
vvv rdf:type uuu .
|
vvv rdf:type xxx . |
| rdfs10 |
uuu rdf:type rdfs:Class . |
uuu rdfs:subClassOf uuu . |
| rdfs11 |
uuu rdfs:subClassOf vvv .
vvv rdfs:subClassOf xxx .
|
uuu rdfs:subClassOf xxx . |
| rdfs12 |
uuu rdf:type rdfs:ContainerMembershipProperty . |
uuu rdfs:subPropertyOf rdfs:member . |
| rdfs13 |
uuu rdf:type rdfs:Datatype . |
uuu rdfs:subClassOf rdfs:Literal . |
A komplettség kimondása
ezekre a szabályokra nagyobb óvatosságot igényel, mivel egy gráf
rdfs-inkonzisztens lehet azon az alapon, hogy kielégíthetetlen állításokat
tartalmaz rosszul tipizált XML-literálokról. Például:
<ex:a> rdfs:subClassOf rdfs:Literal .
<ex:b> rdfs:range <ex:a> .
<ex:c> rdfs:subPropertyOf <ex:b>.
<ex:d> <ex:c> "<"^^rdf:XMLLiteral .
ahol követelmény, hogy a rosszul tipizált XML-literál jelentése ne egy
literál-érték legyen, de a többi állítás alapján mégis kikövetkeztethető,
hogy az. Minthogy egy ilyen rdfs-inkonzisztens gráf rdfs-következménye minden RDF gráf, még akkor is,
ha ezek szintaktikailag függetlenek az előzménytől, ki kell zárnunk ezt az
esetet.
Van egy tipikus jele az inkonzisztenciának, ami felismerhető a
következmény szabályokkal, az alábbi formájú triplet levezetésével:
xxx rdf:type rdfs:Literal .
ahol xxx hozzá van rendelve
egy rosszul tipizált XMLliterálhoz az lg
szabály segítségével. Nevezzük ezt a tripletet egy XML
ütközésnek. Egy ilyen ütközés levezetése a fenti példából igen
egyszerű:
<ex:d> <ex:c> _:1 . (az lg szabály alapján, ahol _:1
hozzá van rendelve
"<"^^rdf:XMLLiteral)-hoz
<ex:d> <ex:b> _:1 . (az rdfs7 szabály alapján)
_:1 rdf:type <ex:a>. (az rdfs3 szabály alapján)
_:1 rdf:type rdfs:Literal . (az rdfs9 szabály alapján)
Ezek a szabályok ezután komplettek a következő értelemben:
RDFS-következmény lemma. S rdfs-következménye E, ha és csak akkor, ha
létezik egy olyan gráf, mely levezethető S-ből plusz az RDFS axiomatikus tripletekből az lg szabály, a gl szabály, az RDF- és RDFS
következmény-szabályok alkalmazásával, és amelynek egyszerű következménye E, vagy pedig tartalmaz egy XML
ütközést. (Bizonyítás
az A. függelékben)
Az RDFS szabályok is bizonyos mértékig redundánsak: például, az RDF axiomatikus tripletek,
egy kivételével, levezethetők az rdfs2 és rdfs3
szabályokból, valamint az RDFS axiomatikus tripletekből.
Ezeknek a szabályoknak az outputjai gyakran újabb outputokat váltanak ki.
Ezek a szabályok végig fogják vinni az összes rdf:type állítást,
felfelé a gráfban, az altulajdonság- és alosztály-hierarchiákra, majd újra
kijelentik ezt a tulajdonságot a főtulajdonságokra és főosztályokra is. Az rdf1 szabály rdf:type
kijelentéseket generál a gráfban szereplő minden tulajdonságnévre, az rdfs3 az utolsó RDFS axiomatikus triplettel pedig megadja
az rdf:type kijelentéseket az összes használt osztálynévre.
Minden altulajdonság- és alosztály-kijelentés megfelelő rdf:type
kijelentéseket generál az alanya és a tárgya számára az rdfs2 és rdfs3
szabályok, valamint az RDFS axiomatikus tripletek halmazában lévő
"érvényességi kör" és "értéktartomány" (domain és range) kijelentések
segítségével. A szabályok ilyen formátumú állításokat fognak generálni:
uuu rdf:type rdfs:Resource .
minden uuu számára V-ben, valamint ilyen formátumúakat:
uuu rdfs:subClassOf rdfs:Resource .
minden uuu osztálynév számára; továbbá több 'univerzális' tényt, mint
pl:
rdf:Property rdf:type rdfs:Class .
7.3.1 Az extenzionális
következmény szabályai
Az erősebb extenzionális szemantikai feltételek, amelyeket a 4.1 szekcióban ismertettünk,
további következményeket is érvényessé tesznek, amelyeket nem fednek le az
RDFS szabályok. Az alábbi táblázat felsorol néhány következménymintát,
amelyek érvényesek ebben az erősebb szemantikában. Ez azonban nem a teljes halmaza az extenzionális
szemantikai feltételek szabályainak. Megjegyezzük, hogy e szabályok egyike
sem rdfs-érvényes; ezek csak azokra a szemantikai feltételekre vonatkoznak,
amelyek a 4.1 szekcióban
leírt, megerősített szemantikai feltételeket alkalmazzák. Ezeknek a
szabályoknak egyéb következményei is vannak, mint pl. hogy az
rdfs:Resource lesz minden tulajdonság érvényességi köre és
értéktartománya is.
Az ext5-ext9 szabályok egy közös mintát követnek; ezek tükrözik azt a
tényt, hogy a megerősített extenzionális feltételek megkövetelik: az rdfV és
rdfsV szókészletekben lévő tulajdonságok érvényességi köre (tranzitív
tulajdonságoknál az értéktartománya is) olyan széles legyen, amilyen csak
lehet, hogy bármilyen kísérletet, mely a korlátozásukra irányul, a
szemantikai feltételek "aláaknázhassanak". Hasonló szabályok érvényesek az
rdfs:range és az rdfs:domain főtulajdonságaira is.
Nem valószínű, azonban, hogy az ilyen esetek bármelyike felmerül a
gyakorlatban.
Néhány további következtetés, mely érvényes lenne az RDFS szemantikai
feltételek extenzionális változatában
| ext1 |
uuu rdfs:domain vvv .
vvv rdfs:subClassOf zzz .
|
uuu rdfs:domain zzz . |
| ext2 |
uuu rdfs:range vvv .
vvv rdfs:subClassOf zzz .
|
uuu rdfs:range zzz . |
| ext3 |
uuu rdfs:domain vvv .
www rdfs:subPropertyOf uuu . |
www rdfs:domain vvv . |
| ext4 |
uuu rdfs:range vvv .
www rdfs:subPropertyOf uuu . |
www rdfs:range vvv . |
| ext5 |
rdf:type rdfs:subPropertyOf
www .
www rdfs:domain vvv .
|
rdfs:Resource rdfs:subClassOf vvv
. |
| ext6 |
rdfs:subClassOf
rdfs:subPropertyOf www .
www rdfs:domain vvv .
|
rdfs:Class rdfs:subClassOf vvv
. |
| ext7 |
rdfs:subPropertyOf
rdfs:subPropertyOf www .
www rdfs:domain vvv .
|
rdf:Property rdfs:subClassOf vvv
. |
| ext8 |
rdfs:subClassOf
rdfs:subPropertyOf www .
www rdfs:range vvv .
|
rdfs:Class rdfs:subClassOf vvv
. |
| ext9 |
rdfs:subPropertyOf
rdfs:subPropertyOf www .
www rdfs:range vvv .
|
rdf:Property rdfs:subClassOf vvv
. |
7.4 Az adattípus-következmény
szabályai
Hogy az állítások és a következmény-szabályok értelmében megragadhassuk az
adattípus-következményt, a
szabályoknak olyan információkra kell hivatkozniuk, amelyeket maguk az adattípusok szolgáltatnak; és hogy ki
tudjuk mondani ezeket a szabályokat, olyan szintaktikai kondíciókat kell
feltételeznünk, amelyek csak az adattípus-források lekérdezése útján ellenőrizhetők.
Minden fajtájú információ számára, mely egy adattípusról hozzáférhető, egy ennek megfelelő
következtetési szabályt lehet kimondani, amit úgy foghatunk fel, mint az RDFS
következmény-szabályok táblázatának kibővítését. Ezeket a szabályokat úgy
kell érteni, hogy olyan adattípusokra érvényesek, amelyek nem beépített
adattípusok (vagyis nem olyanok, amelyek szabályai már eleve az RDFS
következmény-szabályok részét képezik). Az alábbi táblázatban megadott
szabályok feltételezik, hogy információ áll rendelkezésre arról az adattípusról, amelyet egy felismert
URI hivatkozás reprezentál, és ezzel az URI-vel hivatkoznak erre az
információra (az adattípusban).
Az alapvető információ minden egyes literál karakterlánc számára
specifikálja, hogy az legális lexikális formája-e az adattípusnak, vagy sem,
azaz olyan-e, amelyből az adattípus lexikális-érték leképezése egy érvényes
adat-értéket képes kiszámítani. Ez megfelel az alábbi szabálynak, minden sss
karakterláncra, mely legális lexikális formája a ddd által reprezentált adattípusnak:
| rdfD1 |
ddd rdf:type rdfs:Datatype .
uuu aaa "sss"^^ddd .
|
_:nnn rdf:type ddd .
ahol _:nnn egy üres csomópont, mely hozzá van rendelve az "sss"^^ddd-hez az lg szabály segítségével.
|
Tételezzük fel ismertnek, hogy két lexikális forma sss és ttt ugyanarra az
értékre képeződik le a ddd által reprezentált adattípus hatálya alatt; ekkor a következő szabály
érvényesül:
| rdfD2 |
ddd rdf:type rdfs:Datatype .
uuu aaa "sss"^^ddd .
|
uuu aaa "ttt"^^ddd . |
Tételezzük fel ismertnek, hogy a ddd által reprezentált adattípus sss lexikális formája, és az eee által
reprezentált adattípus ttt
lexikális formája ugyanarra az értékre képeződik le. Ekkor a következő
szabály érvényes:
| rdfD3 |
ddd rdf:type rdfs:Datatype .
eee rdf:type rdfs:Datatype .
uuu aaa "sss"^^ddd .
|
uuu aaa "ttt"^^eee . |
Továbbá, ha ismert, hogy a ddd által reprezentált adattípus értéktere részhalmaza az eee által
reprezentált adattípus
értékterének, akkor jogosan állítható, hogy:
ddd rdfs:subClassOf eee .
ám ezt explicit módon ki kell jelenteni, mert pusztán a részhalmaz
relációból ez nem következtethető.
Ha feltételezzük, hogy az ezekbe a szabályokba bekódolt információ helyes,
akkor ezeknek, és a korábbi szabályoknak az alkalmazása egy olyan gráfot
produkál, mely D-következménye
lesz az eredeti gráfnak.
Az rdfD2 és rdfD3 szabályok lényegében helyettesítések a lexikális formák
közötti egyenlőségek alapján. Ezek az egyenlőségek képesek lehetnek
végtelenül sok konklúzió előállítására (például lehetőségünk van akármennyi
vezető nullát hozzáadni az xsd:integer bármelyik lexikális
formájához anélkül, hogy az megszűnne korrekt xsd:integer
lexikális forma lenni). Hogy elkerüljük az ilyen korrekt, de haszontalan következtetéseket, elegendő az
rdfD2 szabályt olyan esetekre korlátozni, amelyek felváltják a lexikális
formát a szóban forgó adattípus
kanonikus formájával (ahol definiáltak ilyen kanonikus formát). De, hogy ne
hagyjunk ki érvényes következményeket, az ilyen kanonicizáló szabályokat
alkalmazni kellene minden tervezett következtetés előzményére és
következményére egyaránt, továbbá a megfelelő rdfD3 típusú szabályoknak
tükrözniük kellene a különböző adattípusok kanonikus formái közötti azonosság
ismeretét.
Egyes esetekben más információk is hozzáférhetők lehetnek, amelyek
kifejezhetők egy külön RDFS szókészlet segítségével. Szemantikai
kiterjesztések szintén definiálhatnak további ilyen adattípus-specifikus
jelentéseket.
Ezek a szabályok lehetővé teszik, hogy arra a következtetésre jussunk,
hogy bármilyen, felismert adattípussal rendelkező 'jól formált' tipizált
literál jelent valamit az rdfs:Literal osztályban.
<ex:a> <ex:p> "sss"^^<ex:dtype> .
<ex:dtype> rdf:type rdfs:Datatype .
<ex:a> <ex:p> _:nnn . (az lg szabály alapján)
_:nnn rdf:type <ex:dtype> .
<ex:dtype> rdfs:subClassOf rdfs:Literal .
_:nnn rdf:type rdfs:Literal .
Az rdfD1 elegendő ahhoz, hogy felszínre hozza az adattípus-ütközés néhány esetét az alábbi
formátumú következtetési lánc segítségével:
<ex:p> rdfs:range <ex:dtype> .
<ex:a> <ex:p> "sss"^^<ex:otherdtype> .
<ex:a> <ex:p> _:nnn .
_:nnn rdf:type <ex:otherdtype> . (az rdfD1 szabály alapján)
_:nnn rdf:type <ex:dtype> . (az rdfs3 szabály alapján)
Lehet, hogy ezek a szabályok nem nyújtják a következtetési alapelvek
komplett halmazát a D-következmény kiszámításához, mivel előfordulhatnak
olyan érvényes D-következmények egyes adattípusokra, amelyek ezeknek az
adattípusoknak a sajátos tulajdonságaitól függenek, mint pl. az értéktér
mérete (pl. az xsd:boolean csak két elemmel rendelkezik, s ezért
minden, amit megállapítunk erre a két értékre, annak igaznak kell lennie az
összes ilyen adattípussal rendelkező literálra.) Különösen, az xsd:string XSD
adattípus értéktere és lexikális formáról értékre történő leképezése
szentesíti a tipizált literálok azonosítását a nyelv-tegekkel nem rendelkező,
típus nélküli literálokkal, minden olyan karakterlánc esetén, mely belefér az
adattípus lexikális terébe, minthogy mindkettő azt a Unocode karakterláncot
jelenti, ami ki van írva literálban; így az alábbi következtetési szabály
érvényes minden XSD-interpretáció esetén (itt az 'sss' egy tetszőleges RDF
karakterláncot jelöl az xsd:string
| xsd 1a |
uuu aaa "sss". |
uuu aaa "sss"^^xsd:string . |
| xsd 1b |
uuu aaa "sss"^^xsd:string . |
uuu aaa "sss". |
Hasonlóan ahhoz, amit fentebb, az rdfD2 és rdfD3 szabályokról mondtunk, az
alkalmazások szisztematikusan behelyettesíthetik ezen ekvivalens formák
egyikét a másikával, ahelyett, hogy közvetlenül alkalmaznák őket.
"A bizonyítás egyik érdeme, hogy felébreszt egy bizonyos kételyt a
vizsgált eredménnyel kapcsolatban." – (Bertrand Russell).
Üres gráf
lemma. A tripletek üres halmaza bármely gráf következménye lehet, de
a tripletek üres halmazának következménye csak önmaga lehet.
Bizonyítás. Legyen N tripletek egy üres halmaza. A
gráfra vonatkozó szemantikai feltételek előírják, hogy N legyen igaz I-ben,
minden I-re; ekkor az első rész a következmény definíciójából levezethető.
Tételezzük fel, hogy G egy bármilyen nem-üres gráf, és s p o . egy triplet
G-ben; ekkor egy I interpretáció, ahol IEXT(I(p)) = { } nem elégíti ki G-t,
kielégíti azonban N-t; így tehát N-nek nem lehet következménye G.
QED
[QED = "quod erat demonstrandum" = "ezt kellett
bizonyítani"]
Ez azt jelenti, hogy a későbbi eredmények legtöbbje triviális az üres
gráfok esetén, s ez éppen az, amire számítottunk.
Részgráf lemma. Egy
gráfnak következménye minden részgráfja.
Bizonyítás. Nyilvánvaló a részgráf és a következmény definícióiból. Ha a gráf igaz I-ben,
akkor valamely A-ra, minden tripletje igaz I+A-ban, így a tripletek minden
részhalmaza igaz I-ben. QED
Egyesítési
lemma. RDF gráfok egy S halmazának egyesítése: S-nek következménye, S minden tagja pedig az
egyesítés következménye.
Bizonyítás. Nyilvánvaló a következmény és a gráf-egyesítés definíciójából. S
minden eleme igaz, ha és csak akkor, ha S egyesítésében minden triplet
igaz. QED
Ez azt jelenti, hogy – amint a szöveg is megjegyezi –, a
gráfok egy halmaza ugyanúgy kezelhető, mint egyetlen gráf, amikor a
kielégítés és a következmény kérdését tárgyaljuk. Ezt a konvenciót fogjuk
alkalmazni e függelék további részében is, ahol egy hivatkozást egy
gráfhalmaz interpretációjára (vagy gráfok olyan halmazára, amelynek
következménye egy gráf stb.) minden esetben úgy kell érteni, mint gráfok
halmazának egyesítésére való hivatkozást; amikor pedig 'gráfra'
hivatkozunk a továbbiakban, akkor ezt gráfokra vagy gráfhalmazokra értjük.
Példány lemma. Egy
gráf következménye bármelyik példányának.
Bizonyítás. Tegyük fel, hogy valamely I kielégíti E'-t, és E' egyik példánya E-nek. Ekkor valamilyen E'
üres csomópontjaira történő A leképezés esetén I+A kielégít minden
tripletet E'-ben. E-ben minden b üres csomópontra definiáljuk, hogy
B(b)=I+A(c), ahol c az az üres csomópont vagy név, amellyel b-t helyettesítjük E'-ben, vagy pedig
c=b, amennyiben nem történt helyettesítés. Ekkor I+B(E)=I+A(E')=igaz, tehát
I kielégíti E-t. De mivel I tetszőleges volt, ezért E' következménye E. QED.
A Skolemizáció egy, az automatikus
következtetőrendszerekben gyakran használt szintaktikai transzformáció,
amelyben az egzisztenciális változókat 'új' függvényekkel – másutt még
nem használt függvénynevekkel – helyettesítjük, amelyeket minden
befogadó univerzális változóra alkalmazunk. Az RDF-ben a Skolemizálás azt
jelenti, hogy egy gráfban minden üres csomópontot egy 'új' névvel, azaz egy
URI hivatkozással helyettesítünk, amelyről garantálható, hogy másutt nem
fordul elő. Ez a transzformáció valójában 'tetszőleges' neveket ad a névtelen
entitásoknak, amelyeknek a létezését az üres csomópont használata mintegy
"állítja": a nevek véletlenszerűsége biztosítja, hogy ezekből semmi sem lesz
kikövetkeztethető, ami nem következne a puszta létezésük állításából, amit az
üres csomópontok használata reprezentál. (Literálok használata itt nem volna
megfelelő. A literálok sohasem 'újak' a megkívánt értelemben.)
Precízebben fogalmazva: E-nek egy Skolemizációja (V-re vonatkozóan) E-nek
egy V-re vonatkozó alap-példánya 1:1 arányú példányleképezéssel, mely G
minden üres csomópontját egy olyan URI hivatkozásra képezi le, amely nem
fordul elő G-ben (így a V Skolem-szókészlet és az E szókészlete diszjunkt
halmazok).
Noha maga a Skolemizáció nem szigorúan érvényes művelet, de nem ad semmilyen új tartalmat egy
kifejezéshez, abban az értelemben, hogy egy Skolemizált kifejezés
következményei ugyanazok, mint az eredeti kifejezésé, feltéve, hogy nem
tartalmaznak neveket a Skolem-szókészletből:
Skolemizációs
lemma. Tegyük fel, hogy sk(E) egy Skolemizációja E-nek, V-re
vonatkoztatva. Ekkor sk(E) következménye E; és ha sk(E) következménye F, úgy,
hogy F és V diszjunktak, akkor E következménye F.
Bizonyítás. sk(E) következménye E a Példány
lemma alapján.
Most tételezzük fel, hogy sk(E) következménye F, ahol V és F
szókészletének nincs közös részhalmaza; tételezzük fel továbbá, hogy I
valamilyen interpretáció, mely kielégíti E-t. Ekkor E üres csomópontjairól
történő valamilyen A leképezés esetén I+A kielégíti E-t. Definiáljuk az
sk(E) szókészlet egy I' interpretációját a következőképpen: IR'=IR,
IEXT'=IEXT, I'(x)=I(x) x-re az E szókészletben, és I'(x)=[I+A](y) x-re a V
szókészletben, ahol y az az üres csomópont E-ben, amelyet x-szel
helyettesítettünk be sk(E)-ben. Nyilvánvaló, hogy I' kielégíti sk(E)-t, így
I' kielégíti F-et is. Azonban I'(F)=[I+A](F), minthogy F és V szókészlete
diszjunkt; ily módon I kielégíti F-et. De I tetszőleges volt; így E
következménye F. QED.
Intuitíve, ez a lemma azt mutatja meg, hogy egy Skolemizáció kijelentése
sok tekintetben ugyanolyan tartalmat fejez ki, mint az eredeti gráf
kijelentése. Azonban egy gráfot nem tekinthetünk a Skolemizációjával
egyenértékűnek, hiszen ezek a 'tetszőleges' nevek, ha már publikáltuk őket,
ugyanolyan státussal rendelkeznek, mint bármelyik URI hivatkozás. Továbbá, a
Skolemizáció nem lenne megfelelő művelet ha bármi másra alkalmaznánk, mint a
következmény előzményére. Egy kereső kifejezés Skolemizációja egy teljesen
más kereső kifejezést eredményezne. Mindazonáltal, sok esetben, amikor egy
következtetés eredményét vizsgáljuk, elegendő csak az alapgráfokat tekintetbe
venni: például, feltéve, hogy E nem tartalmaz semmilyen Skolem-szókészletet,
S következménye E, ha és csak akkor, ha S' következménye E.
Az ezután következő lemmák bizonyítása azt az utat követi, hogy egy gráf
interpretációjának felépítésében felhasználja a gráfban magában lévő
lexikális elemeket. (Ez Herbrand
ötlete volt; de itt némileg módosítjuk, hogy megfelelően kezelje a
literálokat.) Ha adva van egy G nem üres gráf, akkor G (egyszerű) Herbrand
interpretációja, amelyet így írunk: Herb(G), az alábbiakban definiált interpretáció lesz:
LVHerb(G) = az összes típus nélküli literál halmaza
G-ben;
IRHerb(G) = az összes olyan név és üres csomópont halmaza, amelyek egy G-ben
lévő triplet alany vagy tárgy pozíciójában előfordulnak;
IPHerb(G) = azon URI hivatkozások halmaza, amelyek egy
G-ben lévő triplet állítmány pozíciójában előfordulnak;
IEXTHerb(G) = {<s,o>: G tartalmaz egy s p o
. tripletet }
ISHerb(G) és ILHerb(G) egyaránt azonosítási
leképezések G szókészletének megfelelő részéire.
|
Nyilvánvalóan, Herb(G)+B, ahol B az azonosítási leképezés G üres
csomópontjaira, kielégít minden tripletet G-ben, a konstrukció által, így
Herb(G) kielégíti G-t.
A Herbrand interpretációk
ugyanúgy kezelik az URI hivatkozásokat, a tipizált literálokat (és az üres
csomópontokat) mint a típus nélküli literálokat, azaz, mintha a saját
szintaktikai formájuk lenne a jelentésük. Persze lehet, hogy ez nem felel meg
az RDF szerzői eredeti szándékának, de a konstrukció azt mutatja, hogy
minden gráf interpretálható ezen az úton. Ezért ez megerősíti, hogy
bármilyen RDF gráfnak van egy kielégítő egyszerű interpretációja, vagyis nem
fordulhat elő egyszerű inkonzisztencia az RDF-ben.
Vegyük észre, hogy G Herbrand interpretációjának univerzuma tartalmazza G
üres csomópontjait; ezek azokat az entitásokat 'szimbolizálják', amelyeknek
ténylegesen a létezését állítják. Mivel az üres csomópontokat úgy kell
interpretálnunk, hogy saját magukat jelentik, ezért ahhoz, hogy kielégítsék a
gráfot, egy gráf Skolemizációjának Herbrand interpretációja izomorf kell hogy
legyen a gráf olyan Herbrand interpretációjával, mely magában foglalja a
Herb(sk(G)) = Herb(G)+B ürescsomópont-leképezést is (ezt a formulát egy
ismert notációs szabálytalansággal írtuk, ahol egy üres csomópontot egy
Herbrand interpretációban úgy kezelünk, mintha egy Skolem-név lenne)
Interpolációs
lemma. S következménye egy E gráf, ha, és csak akkor, ha S egyik
részgráfja E egyik példánya.
Bizonyítás. A "ha" esete levezethető a Részgráf és a
Példány lemmákból.
A "csak akkor, ha" esetre a bizonyítás a Herbrand konstrukciót
használja. Tételezzük fel, hogy S egyszerű következménye E. Herb(S) kielégíti S-t, így Herb(S) kielégíti E-t, vagyis, valamely
A, E üres csomópontjairól IRHerb(S)-re történő leképezés esetén
[Herb(S)+A] kielégíti az összes
s p o .
tripletet E-ben, úgy, hogy S-nek tartalmaznia kell a
[Herb(E)+A](s) p [Herb(E)+A](o) .
tripletet, ami az előző triplet példánya az A példányleképezés szerint. Így
az összes ilyen triplet halmaza egy részgráfja S-nek, mely egy példánya
E-nek. QED
Az alábbiak egyenes következményei az Interpolációs lemmának:
Anonimitási
lemma. Tegyük fel, hogy E egy sovány gráf és E' egy valódi példánya E-nek. Ekkor E' nem
következménye E-nek.
Bizonyítás. Tételezzük fel, hogy E következménye E',
ekkor E egy részgráfja E' egy példánya, s ezért egy valódi példánya E-nek;
így E nem sovány, tehát szemben áll
a feltevéssel. Ezért E-nek nem következménye E'.
QED
Tömörségi
lemma. Ha S következménye E, és E egy véges gráf, akkor S valamely
véges S' részhalmazának következménye E.
Bizonyítás. Az interpolációs lemma alapján, S-nek
valamely S' részgráfja E-nek egy példánya; így S' véges, és S'
következménye E.
QED
Bár a tömörség triviális az egyszerű következmény esetén, ez fokozatosan,
egyre kevésbé lesz triviális a jobban kidolgozott szemantikus
kiterjesztésekben.
Monotonitási lemma. Tegyük fel, hogy
S egy részgráfja S'-nek, és S következménye E. Ekkor S' következménye E. (Az
Általános monotonitási
lemma speciális esete) QED
Általános monotonitási lemma.
Tegyük fel, hogy S, S' RDF gráfok halmazai, úgy hogy S minden eleme az S'
valamelyik elemének a részhalmaza. Tételezzük fel, hogy Y jelzi X-nek egy
szemantikai kiterjesztését, S X-következménye E, továbbá S és E kielégítik Y
minden szintaktikai korlátozását. Ekkor S' Y-következménye E.
Bizonyítás. Elég csupán végigmenni a definíciókon:
tegyük fel, hogy I egy Y-interpretációja S'-nek; ekkor, mivel Y egy
szemantikai kiterjesztése X-nek, I egy X-interpretáció; továbbá, a Részgráf
lemma és az Egyesítési lemma alapján, I kielégíti S-t; így I kielégíti
E-t.
QED
Mindkét alábbi bizonyítás egy közös mintát követ, mely általánosítja az
Interpolációs lemma bizonyításánál alkalmazottat, oly módon, hogy a Herbrand
konstrukció egy olyan módosítására épít, amelyet egy olyan 'klauzúrára'
(closure) alkalmazunk, amelyet a szabályok kimerítő alkalmazásával nyerünk. A
bizonyítások annak a kimutatásával operálnak, hogy az eredményül kapott
interpretáció megfelel a szókészletnek, és hasonlóképpen működnek a Herbrand interpretáció esetében is. E
bizonyítások bonyolultságának jó része abból a kényszerűségből fakad, hogy a
Herbrand konstrukciót adaptálni kell, hogy megfelelően tekintetbe vegye a
literál értékeket. A Herbrand interpretációk ugyanis nem vesznek tudomást a
literálok tipizálásáról, és minden tipizált literált úgy kezelnek, mint
nem-literál értéket; Ez irreleváns, amikor az egyszerű következményre
gondolunk, mely a tipizált literálokat egyszerűen úgy kezeli, mint amelyek
neveket jelentenek; de még nagyobb gondosságra van szükség, amikor rdf- és
rdfs-interpretációkról van szó.
Mindkét bizonyítás egyetlen alapelvre épül, mely egy meglehetősen nehézkes
notációt igényel, de alapvetően egyszerű a megértésük. Az egyszerű Herbrand
interpretáció minden szókészleti elemet úgy kezel, mint amelyik önmagát
jelenti, és az interpretációt ezekből a szintaktikai elemekből építi fel. Az
rdf- és rdfs-interpretációk szemantikai feltételei ezt nem minden esetben
engedik meg: az XML-literáloktól például elvárják, hogy másfajta entitásokat
jelentsenek. Ezért ezekben az esetekben különbséget teszünk a 'valódi'
szemantikai érték, és annak szintaktikai 'pótléka' között, oly módon, hogy
definiálunk egy sur leképezést [sur = surrogate = pótlék]
az interpretáció univerzumáról a gráf szókészletére (plusz az üres
csomópontokra), amely olyan közel áll egy azonosítási leképezéshez, amilyen
közel csak lehet, de amelyik, ha ezekre a speciális literál értékekre
alkalmazzuk, azt a konkrét üres csomópontot azonosítja, mely ennek az
értéknek a tanújaként viselkedik a gráfban. Az RDFS esetében a sur
pótlék-leképezést kiterjesztjük az összes literál értékre, mivel a literálhoz
rendelt üres csomópont megjelenhet az alany pozíciójában, és így információt
rögzíthet a literál értékéről, amelyet azután rá kell alkalmazni erre az
értékre az interpretációban.
RDF-következmény
lemma. S rdf-következménye
E, ha és csak akkor, ha létezik egy olyan gráf, amelyik származtatható S-ből,
plusz az RDF axiomatikus
tripletekből az lg szabályból és
az RDF következmény szabályaiból, és
amelyiknek egyszerű következménye E.
Bizonyítás. A "ha" eset kimutatására csupán azt kell
ellenőrizni, hogy a szabályok rdf-érvényesek-e (ezt gyakorlatképpen az
olvasóra bízzuk); továbbá, ha S vagy E üres, akkor az eredmény triviálisan
adódik; ezért inkább azt tételezzük fel, hogy egyikük sem üres.
Hogy kimutassuk a "csak akkor, ha" esetet, a bizonyítás úgy folytatódik,
hogy megkonstruáljuk S-nek egy RH rdf Herbrand interpretációját,
mely ugyanazt a szerepet tölti be az rdf-interpretációk esetén, mint az
egyszerű Herbrand interpretáció az egyszerű interpretációk setén. Amennyire
lehet, a konstrukció a Herbrand konstrukciót követi, de a jól formált
XML-literálokat úgy interpretálja, hogy azok kielégítsék az RDF szintű
szemantikai feltételeket, azoknak a tripleteknek az útmutatása szerint,
amelyek a C RDF klauzúrában (RDF closure) találhatók, és amelyet
egy olyan gráfként definiálunk, mely az alábbi eljárás eredményeként jön
létre:
- add S-hez az összes RDF axiomatikus tripletet;
- alkalmazd az lg szabályt minden
tripletre, amelyik egy jól tipizált XML-literált tartalmaz, amíg a gráfot
már nem tudja megváltoztatni a szabály;
- alkalmazd az rdf2 szabályt, amíg
a gráf már nem változik;
- alkalmazd az rdf1 szabályt, amíg
a gráf már nem változik;
Megjegyezzük, hogy C pontosan egy új üres csomópontot (_:nnn) tartalmaz
az S-ben lévő minden literál számára, amelyet az lg szabály révén rendelt hozzá a literálokhoz, valamint hogy az
S-ben lévő tripletek minden olyan részgráfja, mely egy jól-tipizált
XML-litrált tartalmaz, pontosan reprodukálásra kerül C-ben az üres
csomóponttal behelyettesített literállal, valamint az
_:nnn rdf:type rdf:XMLLiteral.
extra triplettel együtt, amelyet az rdf2 szabály vezet be. Szintén megjegyzendő, hogy a
bizonyítás csak az lg szabály
alkalmazását igényli a jól tipizált XML-literálokra, úgyhogy ez ténylegesen
valamivel szorosabb eredményre fog vezetni.
Az lg szabály által bevezetett
üres csomópontok pótlékként helyettesítik a jól formált
XML-literálokat a triplet alany pozíciójában. (A következő lemma
bizonyításánál ezt kiterjesztjük az összes literálra.) Hogy
megkonstruálhassunk egy RDF interpretációt, az XML-literálokat és a
pótlékaikat be kell helyettesíteni a megfelelő literál értékekkel az
interpretáció tartományában, azonban a bizonyítás megköveteli, hogy minden
egyes XML literál érték egyedileg kapcsolódjék egy olyan lexikális elemhez,
mely a jelentését hordozza. Ez némi kifinomultságot igényel a következő
konstrukcióban.
Ha lll egy jól formált XML literál, legyen xml(lll) az lll-nek egy XML
értéke; és C-ben bármelyik jól formált XML-literál x XML értéke számára
legyen sur(x) az az üres csomópont, amelyet ehhez az
XML-literálhoz rendeltünk az lg
szabály alkalmazásával; és terjesszük ki sur-t úgy, hogy az
egy azonosítási leképezés legyen az URI hivatkozásokra, üres csomópontokra
és más literálokra C-ben.
RH-t ezek után így definiáljuk:
LVRH = minden típus nélküli literál C-ben plusz
{xml(x): x egy jól tipizált XML-literál S-ben}
IRRH = LVRH plusz az URI hivatkozások,
üres csomópontok és más tipizált literálok halmaza, amelyek
előfordulnak C-ben
IPRH = {x: C tartalmazza az x rdf:type
rdf:Property . tripletet}
Ha x eleme IPRH-nak, akkor IEXTRH(x) =
{<s,o>: C tartalmazza az
s sur(s) x sur(o) . tripletet}
ISRH az azonosítási leképezés az URI hivatkozásokra
S-ben
Ha x egy jól formált XML-literál S-ben, akkor ILRH(x)
= xml(x), egyébként ILRH(x) = x
|
Definiáljunk egy B leképezést a C-ben lévő üres csomópontokra a
következőképpen: B(x)=xml(lll), ha x egy lll jól formált XML
literálhoz van rendelve, egyébként B(x)=x; ekkor nyilvánvaló, hogy [RH+B]
kielégíti C-t és ezért S-t is, és így RH kielégíti S-t.
Mivel C tartalmazza az összes szükséges axiomatikus tripletet, RH
kielégíti mindet.
Könnyen belátható, hogy J, a konstrukciójánál fogva, kielégíti az első
két RDF szemantikai feltételt; az rdf2 szabály által bevezetett tripletek számára
követelmény, hogy IEXTRH(rdf:type) tartalmazzon egy
<xml(lll),rdf:XMLLiteral>-t minden jól tipizált
lll XML-literál számára.
A harmadik RDF szemantikai
feltétel az egyetlen negatív szemantikai feltétel, mely nem
kielégíthető egyszerűen a konstrukció által, ám ez triviális módon
kielégül. A rosszul tipizált XML-literálok önmaguk jelentését hordozzák
RH-ban, és így, a konstrukciónál fogva, kimaradnak LVRH -ból. Az
<lll, rdf:XMLLiteral> pár nem fordulhat elő
IEXTRH(rdf:type)-ban, mert egy literál nem
fordulhat elő az alany helyén; így a feltétel kielégül, tehát RH egy valódi
rdf-interpretáció.
Mivel S rdf-következménye E, RH kielégíti E-t; így valamely A leképezés
(E üres csomópontjairól IRRH-ra) számára [RH+A] kielégít
minden
s p o .
tripletet E-ben, vagyis IEXTRH(p) tartalmazza
<[RH+A](s),[RH+A](o)>-t, azaz C tartalmazza az
sur([RH+A](s)) p sur([RH+A](o)) .
tripletet, de ez egy példánya az első tripletnek az x -->
sur(A(x)) példányleképezés szerint; így C egy részgráfja, E-nek
egy példánya; így tehát C egyszerű következménye E.
QED
Ez a lemma azt is mutatja, hogy bármilyen gráfnak van egy kielégítő
rdf-interpretációja, és a bizonyítás illusztrálja, hogy miként lehet ezt
felépíteni a klauzúra Herbrand interpretációjából a jól formált XML-literálok
megfelelő interpretálásával, valamint annak megengedésével, hogy olyan
tulajdonságok is létezhetnek, amelyeknek nincs kiterjedésük. Jegyezzük meg,
hogy ha E véges, akkor C származtatott részgráfja ugyancsak véges.
Az RDFS-következmény lemma szerkezetileg hasonló az RDF változatához, és
erősen hasonló definíciókat is használ, de természetesen hosszabb annál, és
egy kidolgozottabb konstrukciót igényel, annak biztosítására, hogy az
rdfs:Literal és az rdfs:Resource
osztálykiterjedései minden literál értéket tartalmaznak.
RDFS-következmény lemma. S
rdfs-következménye E, ha és
csak akkor, ha létezik egy olyan gráf, amelyik származtatható S-ből, plusz az
RDF- és RDFS axiomatikus
tripletekből, az lg szabály, a gl szabály, valamint az RDF- és az RDFS-következmény szabályok alkalmazásával, és
amelyiknek vagy egyszerű következménye E, vagy XML ütközést mutat.
Bizonyítás. Ismét, hogy kimutassuk a "ha" esetét,
elegendő kimutatni, hogy az RDFS-következmény szabályai rdfs-érvényesek,
amit ezúttal is gyakorlatként átengedünk az olvasónak; és az üres esetek
itt is triviálisak.
A "csak akkor, ha" eset kimutatása ugyancsak hasonlít az előző lemmában
alkalmazotthoz, sőt hasonló konstrukciót és terminológiát is használunk,
azzal a kivétellel, hogy a D elnevezésű RDFS klauzúrát úgy definiáljuk,
hogy az az alábbi eljárás eredménye:
- add S-hez az összes RDF- és RDFS axiomatikus tripleteket;
- alkalmazd az lg szabályt minden
tripletre, amelyik egy literált tartalmaz, amíg a gráfot már nem tudja
megváltoztatni a szabály;
- alkalmazd az rdf2 és rdfs1 szabályokat, amíg a gráf már
nem változik;
- alkalmazd az rdf1, a gl (!) valamint a fennmaradó RDFS-következmény szabályokat, amíg a
gráf már nem változik.
Eltérően az előző lemmától, ez a bizonyítás azt igényli, hogy az lg szabályt az összes literálra
alkalmazzuk (még a rosszul tipizált literálokra is), továbbá igényli az
inverz gl szabály alkalmazását. A gl szabályt csak az rdfs6 vagy az rdfs10 szabályok alkalmazása után szükséges
használnunk, mivel csak ezek a szabályok képesek egy üres csomópontot az
alany pozícióból a tárgy pozícióba átvinni.
Megjegyezzük, hogy D pontosan egy új üres csomópontot (_:nnn) tartalmaz
az S-ben lévő minden literál számára, amelyet az lg szabály révén rendelt hozzá a literálokhoz, valamint hogy az
S-ben lévő tripletek minden olyan részgráfja, amelyik bármilyen literált
tartalmaz, pontosan reprodukálásra kerül D-ben, az üres csomóponttal
behelyettesített literállal, valamint az
_:nnn rdf:type rdfs:Literal .
extra triplettel, amelyet az rdfs1 szabály vezet be, és esetleg az
_:nnn rdf:type rdf:XMLLiteral .
extra triplettel együtt, amelyet az rdf2 szabály vezet be, ahol szükséges. Ez azt jelenti,
hogy a konstrukcióban ez után a pont után a literálok ténylegesen figyelmen
kívül hagyhatók, mivel az utána következő szabályok bármelyike, amelyik
olyan tripletre vonatkozik, mely literált tartalmaz, ugyanolyan jól
alkalmazható azokra a hasonló tripletekre is, amelyekben a literálokat már
helyettesítettük a hozzájuk rendelt üres csomópontokkal. A bizonyítás
további része ezt úgy alkalmazza, hogy előírja: a literál értékek az
interpretációban csak azokat a szemantikai feltételeket elégítsék ki,
amelyek az olyan üres csomópontokra érvényesek, amelyek hozzá vannak
rendelve a megfelelő literálokhoz, figyelmen kívül hagyva a gráfnak azokat
a tripletjeit, amelyek literálokat tartalmaznak. A gl szabály használata biztosítja, hogy D tartalmaz
minden olyan tripletet, amelyikben van egy literál, ha és csak akkor, ha
tartalmaz egy hasonló tripletet is, amelyben a literál már le van cserélve
a hozzá rendelt üres csomóponttal.
Ugyanúgy, mint az előző bizonyításban: Ha lll egy jól formált XML
literál, legyen xml(lll) az lll-nek egy XML értéke; a sur
pótlék-leképezést ekkor így terjesztjük ki: Először is, a sur
tartománya az a halmaz, mely csak a D-ben előforduló URI hivatkozásokat,
literálokat, üres csomópontokat, valamint a D-ben előforduló jól formált
XML-literálok XML értékeit tartalmazza. (Ez az alább definiált
rdfs-Herbrand interpretáció univerzuma.) Most tehát, ha lll egy jól formált
XML-literál D-ben, legyen sur(xml(lll)) az az üres
csomópont, amelyet lll-hez rendeltünk az lg szabály alkalmazásával; D-ben lévő minden más lll
literál számára legyen sur(lll) az az üres csomópont, amelyet
lll-hez rendeltünk az lg szabály
révén, és D-ben lévő minden URI hivatkozás és üres csomópont számára legyen
sur(x) = x . Jegyezzük meg, hogy a sur tartománya csak
azokat az URI hivatkozásokat és üres csomópontokat tartalmazza, amelyek
előfordulnak D-ben.
S-nek egy SH rdfs-Herbrand interpretációját ezek után az előző
lemmáéhoz hasonlóan konstruáljuk meg:
LVSH = {x: D tartalmazza a sur(x)
rdf:type rdfs:Literal . tripletet}
IRSH = LVSH plusz az URI hivatkozások,
üres csomópontok és literálok (kivéve jól formált XML-literálok)
halmaza, amelyek előfordulnak D-ben.
IPSH = {x: D tartalmazza a
sur(x) rdf:type rdf:Property .
tripletet}
Ha x eleme IPRH-nak, akkor IEXTRH(x) =
{<s,o>: D tartalmazza a
sur(s) x sur(o) . tripletet}
ISSH az azonosítási leképezés az URI hivatkozásokra
S-ben
Ha x egy jól formált XML-literál S-ben, akkor ILSH(x)
= xml(x), egyébként ILSH(x) = x
|
Definiáljuk B(x)-et a következőképpen: ha x egy üres csomópont, mely egy
lll jól formált XML literálhoz van rendelve D-ben, akkor B(x) =
xml(lll); ha ez bármi más lll literálhoz van rendelve D-ben, akkor
B(x)=lll; egyébként pedig B(x)=x; ekkor nyilvánvaló, hogy [SH+B] kielégíti
D-t, és ezért S-t is, és így SH kielégíti S-t.
Ugyanúgy, mint az előző lemmánál, SH kielégíti az összes szükséges RDF
és RDFS axiomatikus tripletet (az első RDF szemantikai feltételt már a
konstrukció révén).
SH kielégíti a harmadik RDF szemantikai feltételt, de csak abban az
esetben, ha D nem tartalmaz XML ütközést. Megjegyezzük, hogy a pótlékok
jelenléte a rosszul tipizált XML literáloknál érvényteleníti azt az érvet,
amelyet az előző lemmánál használtunk, mondván hogy ez a feltétel
triviálisan teljesül. Ezért tételezzük fel, hogy D nem tartalmaz XML
ütközést.
Amint a szövegben megjegyeztük, úgy tekinthetjük az első RDFS
szemantikai feltételt, mint ICEXT és IC definiálását: így járunk el, minden
további megjegyzés nélkül, és minden feltételt az IEXT fogalmával írunk le.
Hogy kimutassuk, hogy SH kielégíti a fennmaradó RDFS szemantikai
feltételeket, esetről esetre bizonyítunk, felhasználva a Herbrand
interpretáció minimalitását és a klauzúra teljességét.
E feltételek mindegyike tükrözhető a szabály alkalmazások megfelelő
sorozatával. Az argumentum általános formáját jól illusztrálja a második RDFS szemantikai feltétel
esete: tételezzük fel, hogy <x,y> eleme
IEXTSH(rdfs:domain)-nek és <u,v> eleme
IEXTSH(x)-nek; akkor D-nek tartalmaznia kell a következő
tripleteket:
sur(x) rdfs:domain sur(y) .
sur(u) x sur(v).
így x-nek egy URI hivatkozásnak kell lennie, így sur(x)=x; és
ekkor az rdfs2 szabály révén,
D-nek ezt a tripletet is tartalmaznia kell:
sur(u) rdf:type sur(y).
így IEXTSH(rdf:type) tartalmazza <u,v>-t ;
tehát a feltétel teljesült.
A többi eset is hasonlóan jár el: a szemantikai feltételt lefordítja egy
derivációra a szabályok és axiomatikus tripletek felhasználásával. Az
argumentum formákat az alábbi táblázat foglalja össze. A szemantikai
feltételek némelyike több alsóbb rendű feltételre van felbontva, és
egyeseknek alosztályuk is van.
[Rövidítések:Az alábbi táblázatban az 'is in' (eleme,
benne van stb.) halmazoperátort az el. szócskával jelöljük, hogy a táblázat
áttekinthetõ maradjon. Pl. az X el. Y, így olvasandó: X eleme Y-nak. Az 'axiomatikus' szót
axiom. formában rövidítjük – a ford.]
| RDFS szemantikai feltétel |
Deriváció |
ha x eleme IR-nek, akkor
<x,rdfs:Resource> el. IEXT(rdf:type) |
URI hivatkozás vagy üres csomópont az alanyban:
x a b
x rdf:type rdfs:Resource |
rdfs4a |
Literál:
_:x rdf:type rdfs:Literal
rdfs:type rdfs:range rdfs:Class
rdfs:Literal rdf:type rdfs:Class
rdfs:Literal rdfs:subClassOf rdfs:Resource
_:x rdf:type rdfs:Resource |
lásd alább
axiom.
rdfs3
rdfs8
rdfs9 |
URI hivatkozás vagy üres csomópont a tárgyban:
a b x
x rdf:type rdfs:Resource |
rdfs4b |
URI hivatkozás az állítmányban:
a x b
x rdf:type rdf:Property
rdf:type rdfs:domain rdfs:Resource
x rdf:type rdfs:Resource |
rdf1
axiom.
rdfs2 |
x el. LV ha és csak akkor, ha
<x,rdfs:Literal> el. IEXT(rdf:type) |
jól tipizált XML-literál lll:
a b lll
_:x rdf:type rdf:XMLLiteral
rdf:XMLLiteral rdfs:subClassOf rdfs:Literal
_:x rdf:type rdfs:Literal |
lg, rdf2, sur(xml(lll))=_:x
axiom.
rdfs9 |
egyéb literál lll :
a b lll
_:x rdf:type rdfs:Literal |
lg, rdfs1, sur(lll)=_:x |
ha
<x,y> el. IEXT(rdfs:domain) és <u,v> el. IEXT(x)
akkor
<u,y> el. IEXT(rdf:type) |
x rdfs:domain y .
u x v .
u rdf:type y . |
rdfs2 |
ha
<x,y> el. IEXT(rdfs:range) és <u,v> el. IEXT(x)
akkor
<v,y> el. IEXT(rdf:type) |
x rdfs:range y .
u x v .
v rdf:type y . |
rdfs3 |
ha
<x,rdf:Property> el. IEXT(rdf:type)
akkor
<x,x> el. IEXT(rdfs:subPropertyOf) |
x rdf:type rdf:Property
x rdfs:subPropertyOf x |
rdfs6 |
ha
<x,rdf:Property> el. IEXT(rdf:type)
<y,rdf:Property> el. IEXT(rdf:type)
<z,rdf:Property> el. IEXT(rdf:type)
<x,y> el. IEXT(rdfs:subPropertyOf)
<y,z> el. IEXT(rdfs:subPropertyOf)
akkor
<x,z> el. IEXT(rdfs:subPropertyOf) |
x rdfs:subPropertyOf y
y rdfs:subPropertyOf z
x subPropertyOf z |
rdfs5 |
ha
<x,y> el. IEXT(rdfs:subPropertyOf)
<u,v> el. IEXT(x)
akkor
<x,rdf:Property> el. IEXT(rdf:type)
<y,rdf:Property> el. IEXT(rdf:type)
<u,v> el. IEXT(y) |
x rdfs:subPropertyOf y
u x v
rdfs:subPropertyOf rdfs:domain rdf:Property
x type rdf:Property
rdfs:subPropertyOf rdfs:domain rdf:Property
y rdf:type rdf:Property
u y v |
axiom. triplet
rdfs2
axiom. triplet
rdfs3
rdfs7 |
ha
<x,rdfs:Class> el. IEXT(rdf:type)
akkor
<x,rdfs:Resource> el. IEXT(rdfs:subClassOf) |
x rdf:type rdfs:Class
x rdfs:subClassOf rdfs:Resource |
rdfs8 |
ha
<x,y> el. IEXT(rdfs:subClassOf)
<u,x> el. IEXT(rdf:type)
akkor
<x,rdfs:Class> el. IEXT(rdf:type)
<y,rdfs:Class> el. IEXT(rdf:type)
<u,y> el. IEXT(rdf:type) |
x rdfs:subClassOf y
u rdf:type x
rdfs:subClassOf rdfs:domain rdfs:Class
x rdf:type rdfs:Class
rdfs:subClassOf rdfs:range rdfs:Class
y rdf:type rdfs:Class
u rdf:type y |
axiom. triplet
rdfs2
axiom. triplet
rdfs3
rdfs9 |
ha
<x,rdfs:Class> el. IEXT(rdf:type)
akkor
<x,x> el. IEXT(rdfs:subClassOf) |
x rdf:type rdfs:Class
x rdfs:subClassOf x |
rdfs10 |
ha
<x,rdfs:Class> el. IEXT(rdf:type)
<y,rdfs:Class> el. IEXT(rdf:type)
<z,rdfs:Class> el. IEXT(rdf:type)
<x,y> el. IEXT(rdfs:subClassOf)
<y,z> el. IEXT(rdfs:subClassOf)
akkor
<x,z> el. IEXT(rdfs:subClassOf) |
x rdfs:subClassOf y
y rdfs:subClassOf z
x rdfs:subClassOf z |
rdfs11 |
ha
<x,rdfs:ContainerMembershipProperty> el. IEXT(rdf:type)
akkor
<x,rdfs:member> el. IEXT(rdfs:subPropertyOf) |
x rdf:type rdfs:ContainerMembershipProperty
x rdfs:subPropertyOf rdfs:member |
rdfs12 |
ha
<x,rdfs:Datatype> el. IEXT(rdf:type)
akkor
<x,rdfs:Literal> el. IEXT(rdfs:subClassOf) |
x rdf:type rdfs:Datatype
x rdfs:subClassOf rdfs:Literal |
rdfs13 |
így tehát SH egy rdfs-interpretáció.
Mivel S rdfs-következménye E, ezért SH kielégíti E-t: így valamely A
leképezés (E üres csomópontjairól IRSH-re) esetén [SH+A]
kielégít minden
s p o .
tripletet E-ben, azaz IEXTSH(p) tartalmazza
<[SH+A](s),[SH+A](o)>-t, vagyis D tartalmazza a
sur([SH+A](s)) p sur([SH+A](o)).
tripletet, mely egy példánya az első tripletnek az x -->
sur(A(x)) példányleképezés szerint, feltéve, hogy o nem literál.
Ha o egy literál, akkor sur([SH+A](o) az az üres csomópont, amely
hozzá van rendelve o-hoz, és így D ezt a tripletet is tartalmazza:
sur([SH+A](s)) p o .
mely egy példánya az első tripletnek az x --> sur(A(x))
példányleképezés szerint. Így D egy részgráfja, E-nek egy példánya az x
--> sur(A(x)) példányleképezés szerint; tehát D egyszerű
következménye E.
Így tehát akár az a helyzet, hogy D egy XML ütközést tartalmaz, akár az,
hogy D egyszerű következménye E, bizonyított, hogy D kielégíti a lemma
feltételeit.
QED
Megjegyzendő, hogy ha E véges, vagy ha D egy XML ütközést tartalmaz, akkor
D-nek egy véges részgráfja szintén kielégíti a lemma feltételeit.
B. függelék: A szakkifejezések
glosszáriuma (Informatív)
[Ebben a szómagyarázatban az
(angol kifejezéseket) tartjuk meg ábécé-sorrendben,
hogy ezek is viszonylag könnyen visszakereshetőek legyenek (a magyar
kifejezések a szövegből a linkek útján közvetlenül is elérhetők) – a
ford.]
Előzmény,
előtétel, előfeltétel, premissza (Antecedent) (fn.) Egy következtetésben az a kifejezés,
vagy azok kifejezések, amely(ek)ből a konklúziót levonjuk. Egy következménye relációban a reláció bal oldala.
Tényállítás,
kijelentés (Assertion) (fn.) (I.) Bármilyen kifejezés,
amelyről azt állítjuk, hogy igaz. (II.) Az a cselekvés, hogy valamiről azt
állítjuk, hogy igaz.
Osztály
(Class) (fn.) Egy általános fogalom, kategória vagy
besorolás. Valami, amit elsődlegesen más dolgok besorolására, vagy
kategorizálására használunk. Formális értelemben: az RDF-ben egy
rdfs:Class típusú erőforrás, a hozzá tartozó olyan erőforrások
halmazával, amelyek mindegyikének rdf:type tulajdonsága ezt az
osztályt kapta értékül. A formális logika irodalmában az osztályokat gyakran
'pedikátumoknak' nevezik.
(Az RDF megkülönbözteti az osztályt a halmaztól noha a
kettő gyakran azonos. Az RDF-ben az osztályok megkülönböztetése a halmazoktól
több szabadságot engedélyez az osztályhierarchiák konstruálásánál, ahogy fentebb már tárgyaltuk.)
Komplett
(Complete) (mn., egy következtetőrendszer jelzőjeként) (1)
Képes felismerni minden következményt két kifejezés között. (2) Képes levonni
minden érvényes következtetést. Használatos ilyen
megszorításokkal is: képes felismerni a következményt, vagy levonni minden érvényes következtetést egy bizonyos korlátozott
formában, vagy esetben (pl. olyan kifejezések között, amelyek valamilyen
normál alakban vannak megadva, vagy amelyek megfelelnek bizonyos szintaktikai
szabályoknak).
(Ezek a definíciók nem pontosan egyenértékűek, mivel az első azt igényli,
hogy a rendszer hozzáférhessen a konklúzióhoz, s így lehet, hogy nem képes
levonni ilyen 'triviális' következtetéseket, mint pl. (p és p) a p-ből.
Jellemzően, egy hatékony gépi következtetőrendszer komplett lehet az első
értelemben, de nem szükségszerűen az a másodikban.)
Konklúzió,
következmény (Consequent) (fn.) Egy következtetésben az a
kifejezés, amelyet az előtétel(ek)ből konstruálunk; egy következménye relációban a reláció
jobb oldala.
Konzisztens
(Consistent) (mn., egy kifejezés jelzőjeként) Kielégítő interpretációval rendelkezik;
nincs belső ellentmondása. (Egy következtetőrendszer jelzőjeként a
korrekt szinonimája.)
Korrekt
(Correct) (mn., egy következtetőrendszer jelzőjeként).
Képtelen levonni bármilyen érvénytelen köveztetést, vagy előállítani egy
hamis következményt. Lásd a következtetés címszónál is.
Eldönthető,
döntésképes (Decideable) (mn., egy következtetőrendszer
jelzőjeként). Véges erőforrások mellett, véges idő alatt képes eldönteni két
kifejezésről, hogy az elsőnek következménye a második. (Egy logika esetében:)
van egy olyan eldönthető következtetési rendszere, amelyik komplett és
korrekt az adott logika szemantikája szempontjából.
(Nem minden logikához tartozik olyan következtetőrendszer, amelyik
komplett és eldönthető is, de még az eldönthető rendszerek is tetszőlegesen
magas számítási komplexitással rendelkezhetnek. A viszony a logikai
szintaxis, a szemantika és a következtetőrendszer komplexitása között még
jelentős kutatások tárgyát képezi.)
Következménye,
következmény (Entail, Entailment) (fn.) Egy
szemantikai viszony két kifejezés között, mely akkor áll fenn, amikor az
elsőnek az igaz volta garantálja a másodiknak az igaz voltát is; amikor
logikailag lehetetlen, hogy az első igaz legyen, ha a második hamis; amikor
bármilyen interpretáció,
amelyik kielégíti az első
kifejezést, szükségszerűen kielégíti a másodikat is. Ilyen szemantikai
viszony érvényes lehet egy kifejezéshalmaz és egy kifejezés között is.
Egyenértékű
(Equivalent) (mn., két dolog viszonyaként) Ugyanazon
feltételek mellett igaz; ha állítás: azonos kijelentést tesz a világról.
Kölcsönösen következményei
egymásnak.
Extenzionális
(Extensional) (mn. egy logika jelzőjeként) egy halmaz alapú
elmélet, vagy egy osztálylogika, amelyben az osztályokat halmazoknak, a
tulajdonságokat <objektum, érték> pároknak tekintjük és így tovább. Egy
olyan elmélet, mely nem enged megkülönböztetést az olyan entitások között,
amelyeknek ugyanaz a kiterjedésük (extenziójuk) (vö. Intenzionális).
Formális
(Formal) (mn.) Olyan nyelven kifejezett, mely elég pontos
ahhoz, hogy hagyományos matematikai módszerekkel eredményeket számíthassunk
ki belőle.
Inkonzisztens
(Inconsistent) (mn.) Hamis bármilyen interpretáció esetén;
lehetetlen kielégíteni.
Inkonzisztencia (Inconsistency) (fn.), bármilyen
inkonzisztens kifejezés vagy gráf.
(A következmény és az
inkonzisztencia szorosan összefügg egymással, hiszen A következménye
B, éppen akkor, amikor (A és nem-B) inkonzisztens
(vö. a következmény második
definíciójával). Ez az alapja sok gépi következtetőrendszernek.
Bár a konzisztencia és
inkonzisztencia definíciói egzakt kettősök, számítási szempontból mégis
eltérőek. Gyakran nehezebb felismerni a konzisztenciát minden szituációban,
mint az inkonzisztenciát felismerni minden szituációban.
Rámutató
(Indexical) (mn., egy kifejezés jelzőjeként)
olyan jelentéssel bír, mely explicit módon a használói környezetre hivatkozik
(mint pl. "itt", "most", "ez").
Következtetés
(Inference) (fn.) Egy cselekvés vagy folyamat, amelynek
során új kifejezéseket konstruálunk meglévő kifejezésekből; egy ilyen
cselekvésnek vagy folyamatnak az eredménye. Azokat a következtetéseket,
amelyek a következményt
produkálják, korrekt vagy érvényes következtetéseknek
nevezzük. Következtetési szabály: egy következtetési típus
formális leírása; következtetőrendszer: következtetési
szabályok szervezett rendszere, vagy olyan szoftver, mely következtetéseket
generál, esetleg következtetések érvényességét ellenőrzi.
Intenzionális
(Intensional) (mn., egy logika jelzőjeként) Nem extenzionális. Olyan logika,
mely megengedi, hogy különböző entitásoknak azonos legyen a kiterjedése
(extenziója).
(Az intenzionalitás hasznossága vagy haszontalansága körül széleskörű vita
folyik a filozófiai logikai irodalomban. Az extenzionális
szemantika-elméletek egyszerűbbek, és a formális logikák konvencionális
szemantikája általában extenzionális nézetet feltételez, ugyanakkor a
hétköznapi nyelvek konceptuális elemzése gyakran azt sugallja, hogy az
intenzionális gondolkodás sokkal természetesebb. Ennek gyakran idézett példái
szerint egy extenzionális logika köteles minden 'üres' osztálykiterjedést
azonosként kezelni, és így azonosnak tekintheti a 'vadkörtét' a 'Mikulással',
továbbá képtelen megkülönböztetni olyan fogalmakat, amelyeknek 'véletlenül'
ugyanazok az egyedeik, mint például az emberi lények, és a kétlábú, szőrtelen
emberszabásúak. Az ebben a dokumentumban leírt szemantika alapvetően
intenzionális.
Interpretáció(ja)
(Interpretation (of)) (fn.) Egy világ azon aspektusainak minimális formális leírása,
melyek éppen elégségesek ahhoz, hogy valamely logika kifejezésének igazságát
vagy hamisságát meg lehessen állapítani.
(egyes logikai szövegek különbséget tesznek egy interpretációs
struktúra között, mely egy 'lehetséges világ', amelyet bármilyen konkrét
szókészlettől független valaminek tekintünk, és egy olyan interpretációs
megfeleltetés között, mely egy szókészletet egy ilyen struktúrára képez
le. Az RDF szemantikája a rövidebb utat választja, amennyiben ezt a kettőt
egyetlen fogalomban egyesíti.)
Logika
(Logic) (fn.) Egy formális nyelv, mely állításokat fejez ki.
Metafizikai, metafizikus
(Metaphysical) (mn.). A dolgok valódi természetével
valamilyen abszolút vagy fundamentális értelemben összefüggő.
Modell-elmélet (Model
Theory) (fn.) Egy formális szemantikai elmélet, mely
kifejezéseket interpretációkkal kapcsol össze.
(A 'modell-elmélet' név a logikai szemantikában meghonosodott használatból
ered, ahol egy kielégítő interpretációt "modell"-nek hívnak. Ez a
szóhasználat azonban gyakran zavarónak tűnik, minthogy majdnem pontosan a
fordítottja annak a jelentésnek, amelyet az ilyen kifejezések takarnak, mint
pl. "számítógépes modellezés", amit ezért el is kerülünk ebben a
dokumentumban.)
Monoton
(Monotonic) (mn., egy logika, vagy egy következtetőrendszer
jelzőjeként) Kielégíti azt a feltételt, hogy ha S következménye E, akkor
(S+T) következménye továbbra is E, azaz, ha további információt adunk
valamilyen előtételhez, az nem tudja érvényteleníteni az előző érvényes következményt.
(Minden logika monoton, mely a konvencionális modell-elméleten és a következmény szabványos
fogalmán alapszik. A monoton logikának az a jellemzője, hogy a következmény
érvényes marad azon a kontextuson
kívül is, amelyben generálták. Az RDF-et is emiatt tervezték monotonnak.)
Nem-monoton
(Nonmonotonic) (mn., egy logika vagy egy
következtetőrendszer jelzőjeként) Nem monoton. Nem-monoton formalizmusokat javasoltak és
alkalmaztak a MI területén és más alkalmazásokban is. A nem-monoton
következtetésre példák lehetnek a következők: alapértelmezett
következtetés (default reasoning), amelynél feltételezünk egy 'normális'
általános igazságot, hacsak ez nem kerül ellentmondásba valamilyen konkrétabb
információval (a madarak általában repülnek, de a pingvinek nem); tagadás
sikertelenség esetén (negation-by-failure): gyakran alkalmazzák logikai
programozási rendszerekben, és az a lényege, hogy ha egy állítás
helyességének bizonyítása valamiért sikertelen, akkor ebből azt a
következtetést vonják le, hogy az állítás hamis; zárt világ implicit
feltételezése (implicit closed-world assumptions):
adatbázis-alkalmazásokban gyakran előforduló feltételezés, amelyből
kiindulva, ha egy korpuszban (vizsgált adathalmazban) egy entitásról hiányzik
valamilyen információ, akkor azt a következtetést vonják le ebből, hogy hibás
az adat, vagy az adatbázis (pl. azt, hogy ha valakinek a neve nem szerepel az
alkalmazottak adatbázisában, akkor az nem is lehet alkalmazott)
(A monoton és nem-monoton következtetések közötti viszony gyakran nehezen
megfogható. Például, ha explicit "zárt világ" feltételtelezést alkalmazunk
azáltal, hogy explicite kijelentjük a korpuszról, hogy komplett, és a
konklúziókban explicit eredetinformációkat adunk meg, akkor a
zártvilág-következtetés monoton; az implicit jelleg az, ami a következtetést
nem-monotonná teszi. A nem-monoton konklúziókról csak valamilyen kontextuson
belül mondhatjuk, hogy érvényesek;
ezek könnyen inkorrekté és félrevezetővé válhatnak ezen a kontextuson kívül.
Ha a kontextust explicitté tesszük a következtetésben, és láthatóvá a
konklúziókban, akkor egy monoton keretbe képezhetjük le a nem-monoton
konklúziókat.)
Ontológiai
(Ontological) (mn.) Filozófia: A ténylegesen
létező dolgok filozófiai tudományával kapcsolatos. Itt:
Valamilyen tématerület formális leírásának részleteivel kapcsolatos.
Állítás,
ítélet (Proposition) (fn.) Valami, ami igazság-értékkel
bír; egy kijelentés vagy kifejezés, ami igaz vagy hamis.
(A nyelv filozófiai elemzésében hagyományosan megkülönböztetjük az
ítéleteket azoktól a kifejezésektől, amelyekkel az ítéleteket kijelentjük; a
modell-elmélet azonban nem igényel ilyen megkülönböztetést.)
Tárgyiasít, megtestesít
(Reify) (ige), tárgyiasítás, megtestesítés
(Reification) (fn.) Tárgyként kategorizál;
entitásként leír. Gyakran olyan konvenciót értünk alatta, amelynél egy
szintaktikai kifejezést szemantikai tárgyként kezelünk, mely egy másik
szintaxissal van leírva. Az RDF-ben egy tárgyiasított triplet nem más, mint
egy triplet azonosítójának és három komponensének leírása más RDF tripletek
segítségével.
Erőforrás
(Resource) (fn.) RDF-ben: (I.) Egy entitás;
bármi az univerzumban (II.) osztálynévként: minden dolgok osztálya; a lehető
legáltalánosabb kategória.
Kielégít
(Satisfy) (tsi.), kielégítő
(Satisfying) (mn., egy interpretáció jelzője) Igazzá tesz.
Az alapvető szemantikai viszony egy interpretáció és egy kifejezés között. Az
X kielégíti Y-t kifejezés azt jelenti, hogy, ha a világ megfelel az X által leírt feltételeknek, akkor
Y-nak igaznak kell lennie.
Szemantikai
(Semantic) (mn.), szemantika
(Semantics) (fn.). A jelentés meghatározásával kapcsolatos.
Gyakran a "szintaktikai" (sintactic) fogalommal szembeállítva
használjuk, a kifejezés, és a jelentése közötti különbség hangsúlyozására.
Skolemizáció, skolemizálás
(Skolemization) (fn.) Egy szintaktikai transzformáció,
amelyben üres csomópontokat "új" nevekkel helyettesítünk.
(Habár nem szigorúan érvényes
művelet, de a Skolemizálás megtartja egy kifejezés lényegi jelentését, és
ezért gyakran alkalmazzuk gépi következtetőrendszerekben. A teljes logikai
forma komplexebb. A fogalom A.
T. Skole logikus/matematikusról kapta a nevét)
Szimbólum, tóken
(Token) (n.) Egy jelkép vagy kifejezés meghatározott
fizikai kiírása a dokumentumban; gyakran szembeállítva a típussal:
egy kifejezés absztrakt nyelvtani formája.
Univerzum
(Universe) (fn.) Az egyetemes osztály, vagy azoknak a
dolgoknak a halmaza, amelyet egy interpretáció létezőknek tekint (az RDF/RDFS
környezetben ez azonos az erőforrások halmazával).
Használ (Use vs.
Mention) (ige, szembeállítva az említ
kifejezéssel) Egy szintaxis darab alkalmazása valaminek a megjelölésére vagy
hivatkozására. A normális formája annak, ahogy a nyelvet használjuk.
("Mindig, amikor egy mondatban valamit ki akarunk mondani egy bizonyos
dologról, akkor használnunk kell ebben a mondatban, nem a dolgot
magát, hanem a nevét, vagy a megjelölését" - Alfred Tarski)
Érvényes, korrekt
(Valid, correct) (mn., egy következtetés vagy következtető
folyamat jelzőjeként) Megfelel egy következménynek, azaz, a következtetés konklúziója az
előtétel következménye.
Jól formált
(Well-formed) (mn., egy kifejezés jelzőjeként) Szintaktikailag
legális.
Világ (World)
(fn.) (a világ:) (I.) A való világ. (egy világ:) (II.) Egy olyan mód, ahogy a
való világ elrendezhető. (III.) Egy interpretáció. (IV.) Egy lehetséges világ.
(A 'lehetséges
világok' fogalmának metafizikai státusa erősen vitatható. Szerencsére nem
kell elköteleznünk magunkat a párhuzamos univerzumokban való hitnek ahhoz,
hogy használhassuk ezt a fogalmat annak II. és III. jelentésében, amelyek
elégségesek a szemantika céljaira.)
C. függelék: Köszönetnyilvánítás
Ez a dokumentum az RDF-mag
Munkacsoport tagjainak közös erőfeszítéseit tükrözi. Különösen jelentős
mértékben járult hozzá ehhez az anyaghoz Jeremy Carroll, Dan Connolly, Jan
Grant, R. V. Guha, Graham Klyne, Ora Lassilla, Brian McBride, Sergey Melnick,
Jos deRoo és Patrick Stickler.
Christopher Menzeltől származik az explicit kiterjedés-leképezés
használatának alapvető ötlete mely lehetővé teszi az önmagára való
alkalmazást anélkül, hogy megsértené a fundáltság axiómát.
Peter Patel-Schneider és Herman ter Horst lényeges problémákat fedeztek
fel a korábbi tervezetekben, és több fontos technikai tökéletesítésre tettek
javaslatot.
Patrick Hayes-nek ezen a dokumentumon végzett munkáját részben a DARPA
támogatta a #2507-225-22. számú szerződés keretében.
- [RDF-FOGALMAK]
- Az RDF Erőforrás Leíró
Keretrendszer alapfogalmai és absztrakt szintaxisa, W3C
Ajánlás, 2004. február 10. Szerkesztők: Klyne G., Carroll J. A mindenkori legutolsó (angol
nyelvű) verzió URL-je: http://www.w3.org/TR/rdf-concepts/.
- [RDF-SZINTAXIS]
- Az RDF/XML
szintaxis specifikációja (átdolgozott kiadás), W3C Ajánlás,
2004. február 10. Szerkesztő: Dave Beckett. A mindenkori legutolsó
(angol nyelvű) verzió URL-je:
http://www.w3.org/TR/rdf-syntax-grammar/ .
- [RDF-TESZTEK]
- Az RDF
tesztsorozata, W3C Ajánlás, 2004. február 10. Szerkesztők:
Grant J., Beckett D. A
mindenkori legutolsó (angol nyelvű) verzió URL-je:
REC-rdf-testcases-20040210.html.
- [RDFMS]
- Resource
Description Framework (RDF) Model and Syntax Specification ,
O. Lassila and R. Swick, Editors. World Wide Web Consortium. 22
February 1999. This version is
http://www.w3.org/TR/1999/REC-rdf-syntax-19990222/. The latest version of RDF
M&S is available at http://www.w3.org/TR/REC-rdf-syntax/.
- [RFC 2119]
- RFC 2119 - Key
words for use in RFCs to Indicate Requirement Levels , S.
Bradner, IETF. March 1997. This document is
http://www.ietf.org/rfc/rfc2119.txt.
- [RFC 2396]
- RFC 2396 -
Uniform Resource Identifiers (URI): Generic Syntax
Berners-Lee,T., Fielding and Masinter, L., August 1998
- [XSD]
- XML Schema Part 2:
Datatypes, Biron, P. V., Malhotra, A. (Editors) World Wide
Web Consortium Recommendation, 2 May 2001
- [OWL]
- Az OWL Web Ontológia
Nyelv – Referencia, W3C Ajánlás, 2004. február 10.
Szerkesztők: Mike Dean and Guus Schreiber . A mindenkori legutolsó (angol
nyelvű) verzió URL-je: http://www.w3.org/TR/owl-ref/ .
- [Conen&Klapsing]
- A
Logical Interpretation of RDF, Conen, W., Klapsing,
R..Circulated to RDF
Interest Group, August 2000.
- [DAML]
- Frank van Harmelen, Peter F. Patel-Schneider, Ian Horrocks (editors),
Reference
Description of the DAML+OIL (March 2001) ontology markup
language
- [Hayes&Menzel]
-
A
Semantics for the Knowledge Interchange Format, Hayes, P.,
Menzel, C., Proceedings of 2001 Workshop on the IEEE
Standard Upper Ontology, August 2001.
- [KIF]
- Michael R. Genesereth et. al., Knowledge
Interchange Format, 1998 (draft American National
Standard).
- [Marchiori&Saarela]
- Query
+ Metadata + Logic = Metalog, Marchiori, M., Saarela, J.
1998.
- [LBASE]
- Lbase:
Semantics for Languages of the Semantic Web, Guha, R. V.,
Hayes, P., W3C Note, 10 October 2003.
- [McGuinness&al]
- DAML+OIL:An
Ontology Language for the Semantic Web, McGuinness, D. L.,
Fikes, R., Hendler J. and Stein, L.A., IEEE Intelligent Systems, Vol.
17, No. 5, September/October 2002.
- [RDF-BEVEZETÉS]
- Az RDF bevezető
tankönyve, W3C Ajánlás, 2004. február 10. Szerkesztők: Frank
Manola and Eric Miller. A
mindenkori legutolsó (angol nyelvű) verzió URL-je
http://www.w3.org/TR/rdf-primer/ .
- [RDF-SZÓKÉSZLET]
- Az RDF Szókészlet Leíró
Nyelv 1.0: RDF Séma, W3C Ajánlás, 2004. február 10.
Szerkesztők: Dan Brickley and R. V. Guha. A mindenkori legutolsó (angol
nyelvű) verzió URL-je: http://www.w3.org/TR/rdf-schema/ .
- [N3]
D.
függelék: Változtatási napló (Informatív)
Változtatások a 2003. december 15-i
Előzetes ajánlástervezet óta.
Az A. függelékben az RDFS következmény lemmáját kijavítottuk. Néhány
elgépelést a glosszáriumban és a fő szövegben szintén korrigáltunk.
Átgondolva ter
Horst észrevételeit, a D-interpretáció definícióját módosítottuk, hogy
alkalmazható legyen egy kiterjesztett szókészletre, beleértve az
adattípus-neveket is.
A változtatási napló régebbi bejegyzéseit eltávolítottuk. Ezek most
megtalálhatók az előző
verzióban


